Czy obciążenia zmienne na każdym typie stropu zachowują się podobnie? Czy obciążenia te pracują tak samo na stropie płytowo-belkowym i np. płytowo-słupowym? A może jest jeden uniwersalny sposób na modelowanie obciążeń zmiennych?
W tym wpisie dowiesz się jaka jest specyfika pracy stropu płytowo-belkowego pod obciążeniem zmiennym oraz nauczysz się jak poprawnie rozkładać te obciążenia.
W poprzednich wpisach z tego cyklu analizowałem strop płytowo-słupowego (zobacz listę wpisów na końcu tekstu). Teraz czas na strop płytowo-belkowy :) Wykorzystując tamtą geometrię stropu zbudowałem strop płytowo-belkowy, na którym dokładnie wyjaśnię Ci jak poszczególne sposoby rozkładu obciążeń zmiennych wpływają na wyniki momentów zginających i ugięć oraz jak uniknąć poważnych błędów w obliczeniach.
Model obliczeniowy stropu płytowo-belkowego
Geometria stropu nie różni się od poprzednich przykładów, z tą różnicą, że poszczególne pola stropu są wydzielone belkami. Tak więc mamy strop płytowo-belkowy o 18-tu polach (rys. 1):
- rozpiętości przęseł w kierunku X od 3.0 do 8.0 m, w kierunku Y rozpiętość stała 5.0 m,
- grubość płyty stropu 0.20 m, belki o przekroju 0.30/0.60 m (górna krawędź zlicowana z górą płyty) oparte na słupach o przekroju 0.30/0.30 m,
- materiał: beton C30/37,
- obciążenie zmienne q = 5.0 kN/m2,
- podział stropu na elementy skończone (ES) pokazałem na rys. 2.
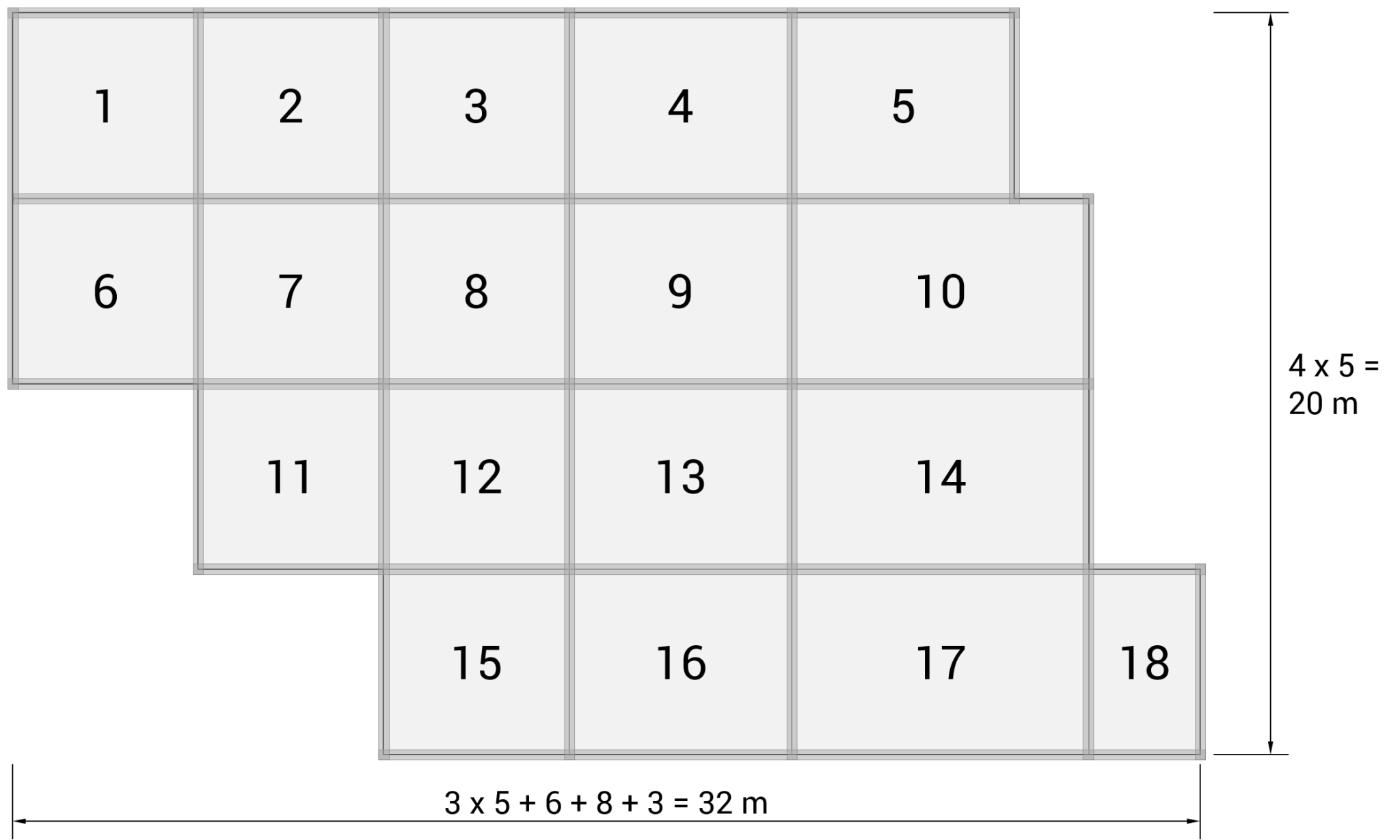
Rys. 1 Geometria stropu i podział pól obciążeń
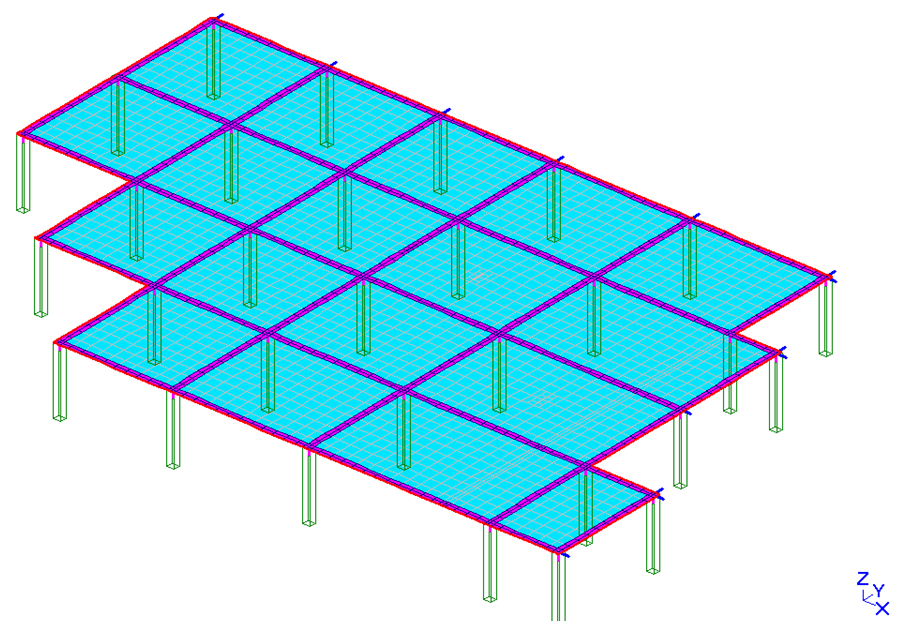
Rys. 2 Model obliczeniowy stropu (3236 ES)
Powierzchnie wpływu
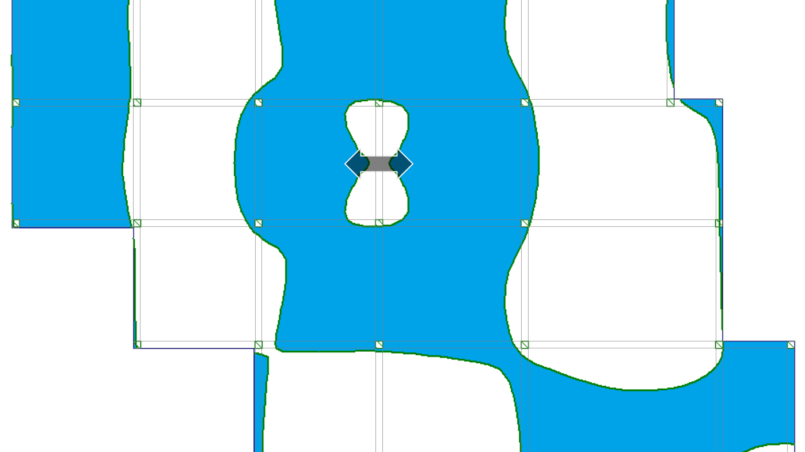
Pamiętasz jak wyznaczyć powierzchnie wpływu dla ugięć i momentów zginających? Jeśli nie, to pomoże Ci w tym wcześniejszy post na ten temat (link: Powierzchnie wpływu). Jest to ważne, żeby zrozumieć zasadę pracy stropu pod obciążeniem. Dzięki powierzchni wpływu możesz stosunkowo łatwo określić, które obszary stropu należy obciążyć, żeby dostać ekstremalne wartości ugięcia, momentu zginającego czy reakcji podporowej jak i innych wielkości.
Tabela 1 przedstawia obrazy powierzchni wpływu stropu płytowo-belkowego dla ugięć i momentów zginających dla czterech charakterystycznych miejsc stropu.
Tab. 1 Przebieg granic powierzchni wpływu dla analizowanych miejsc
| Miejsce | Dla momenty zginającego mx | Dla ugięcia |
|---|---|---|
| a) przęsło wewnętrzne | 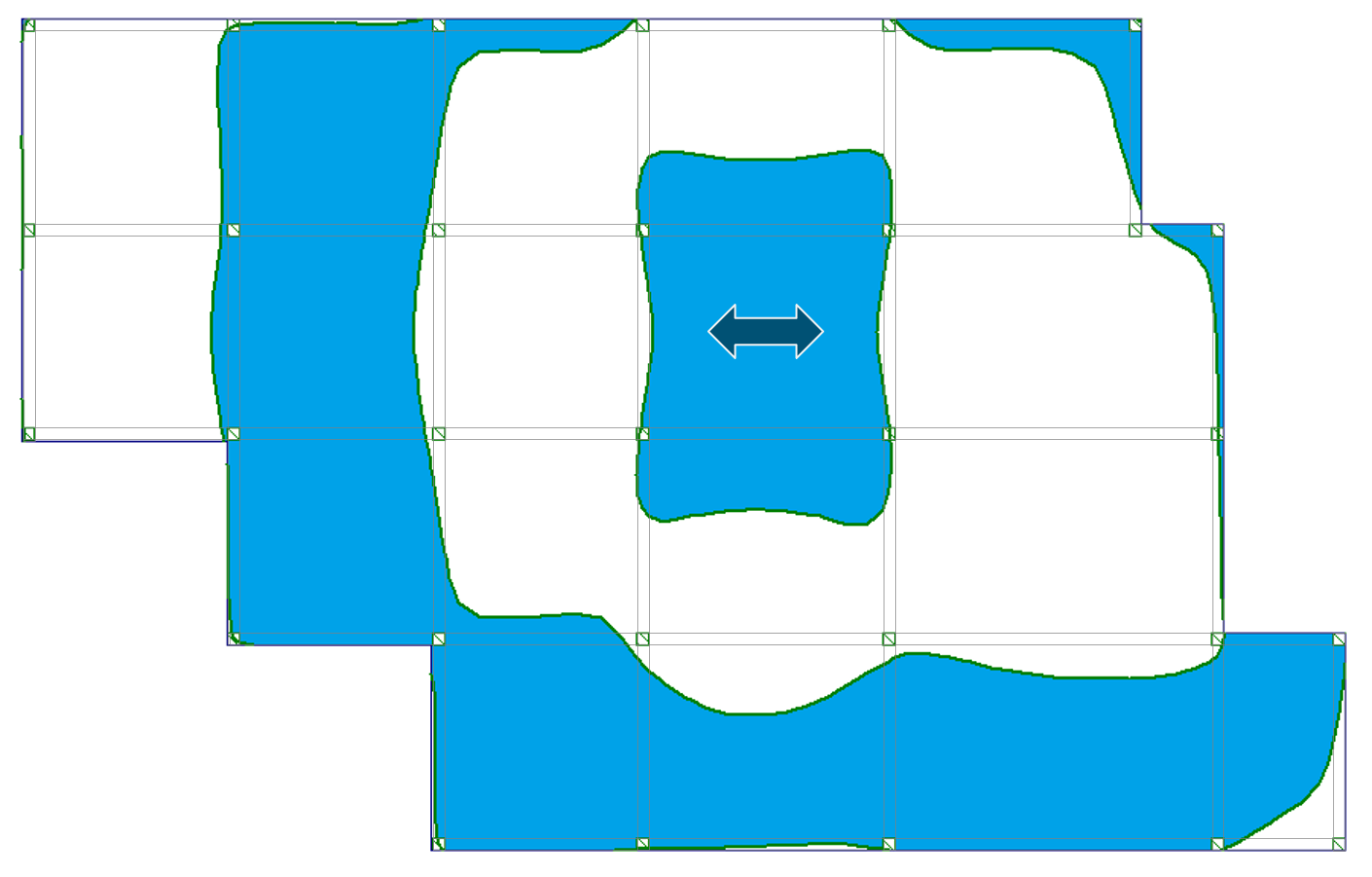 |
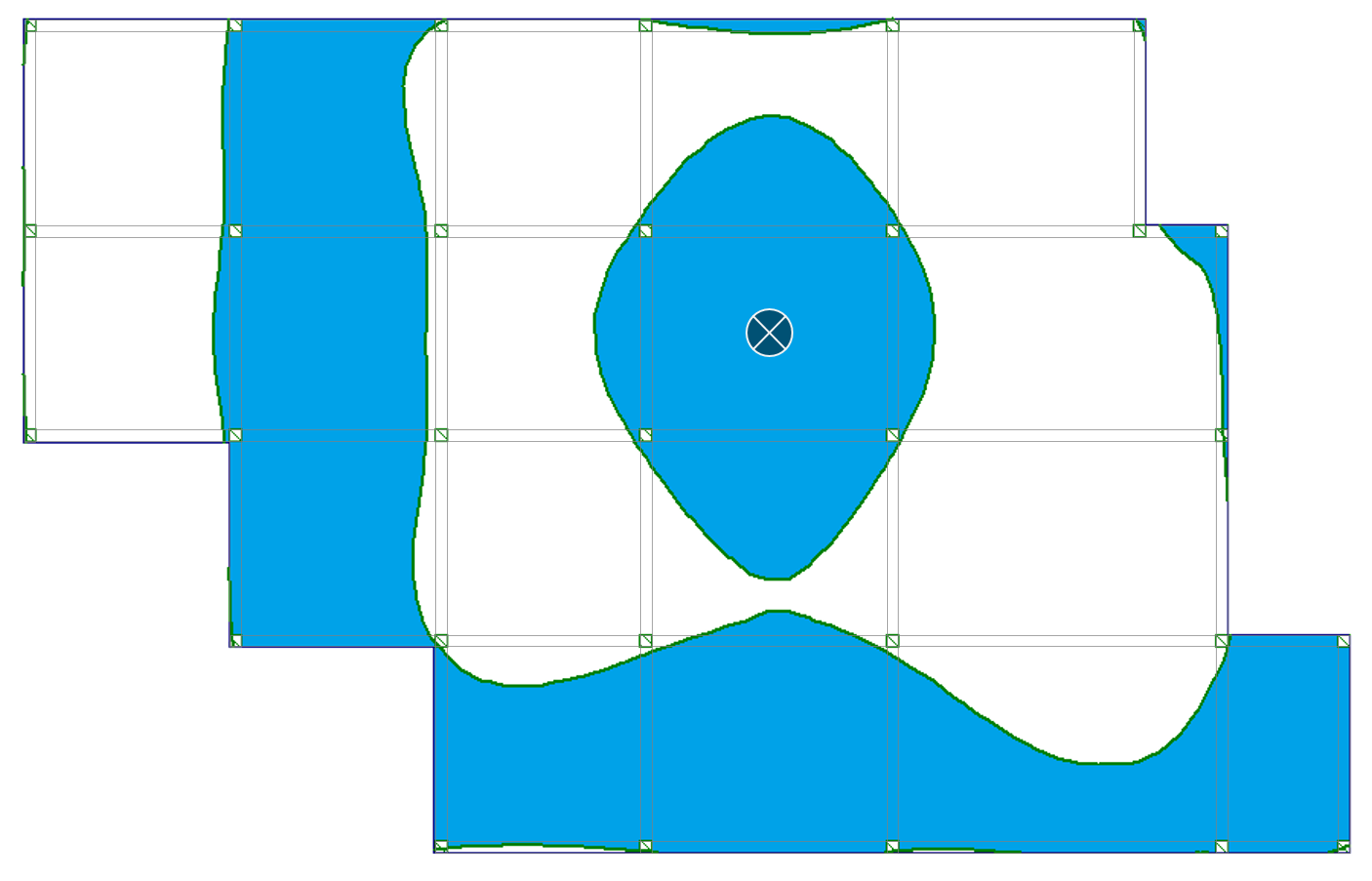 |
| b) przęsło skrajne | 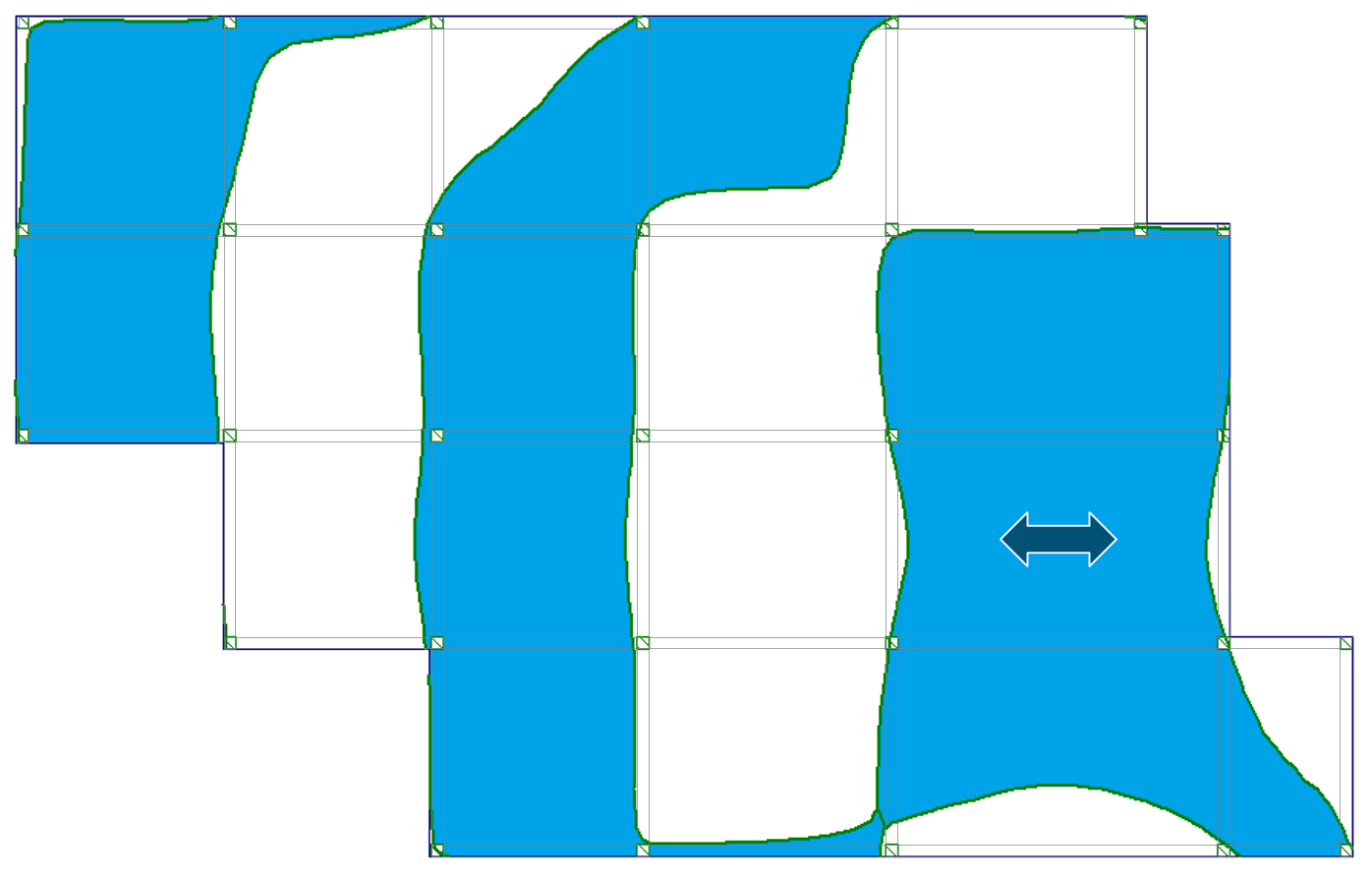 |
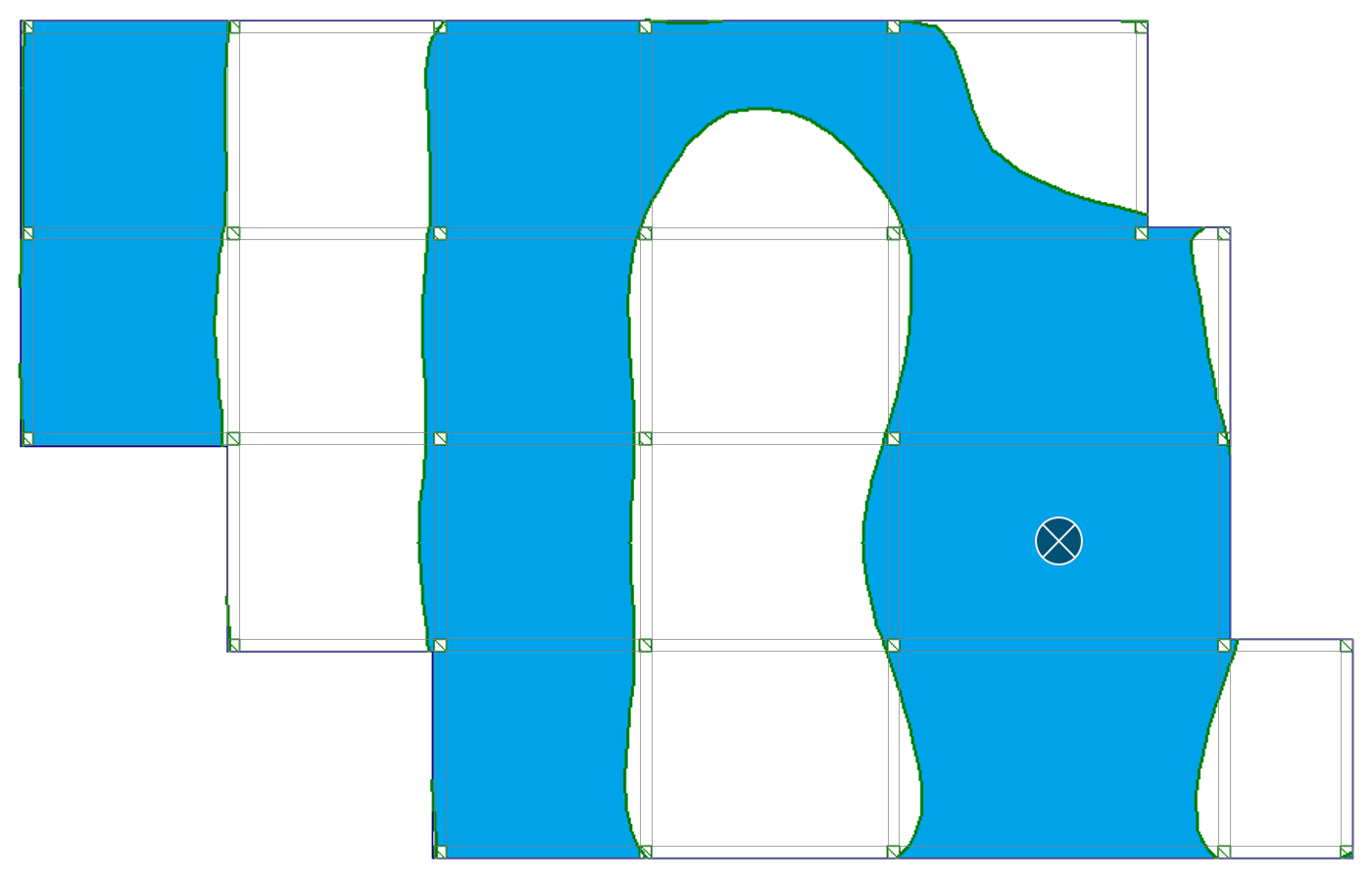 |
| c) w linii podpór (nad belką) | 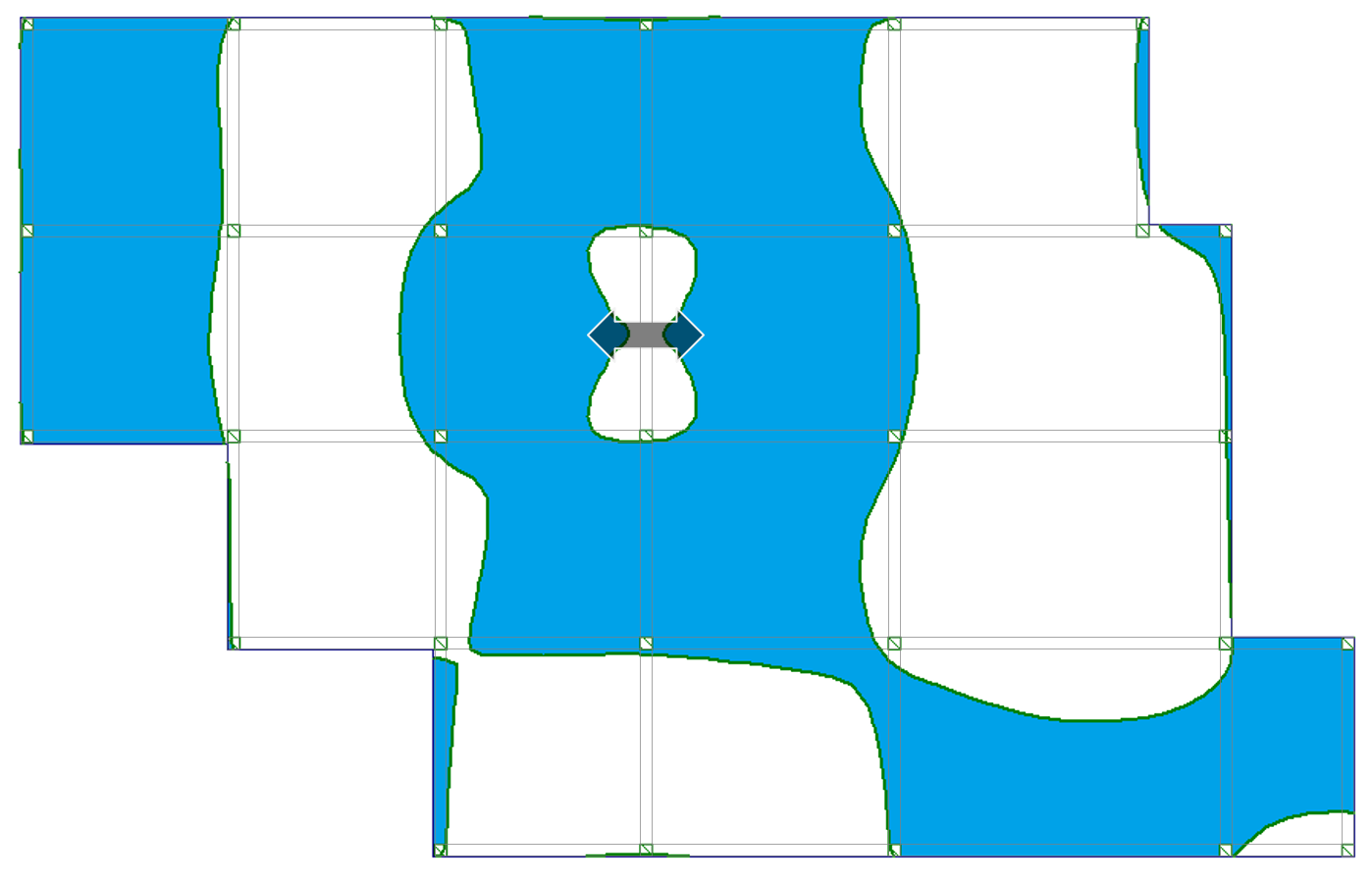 |
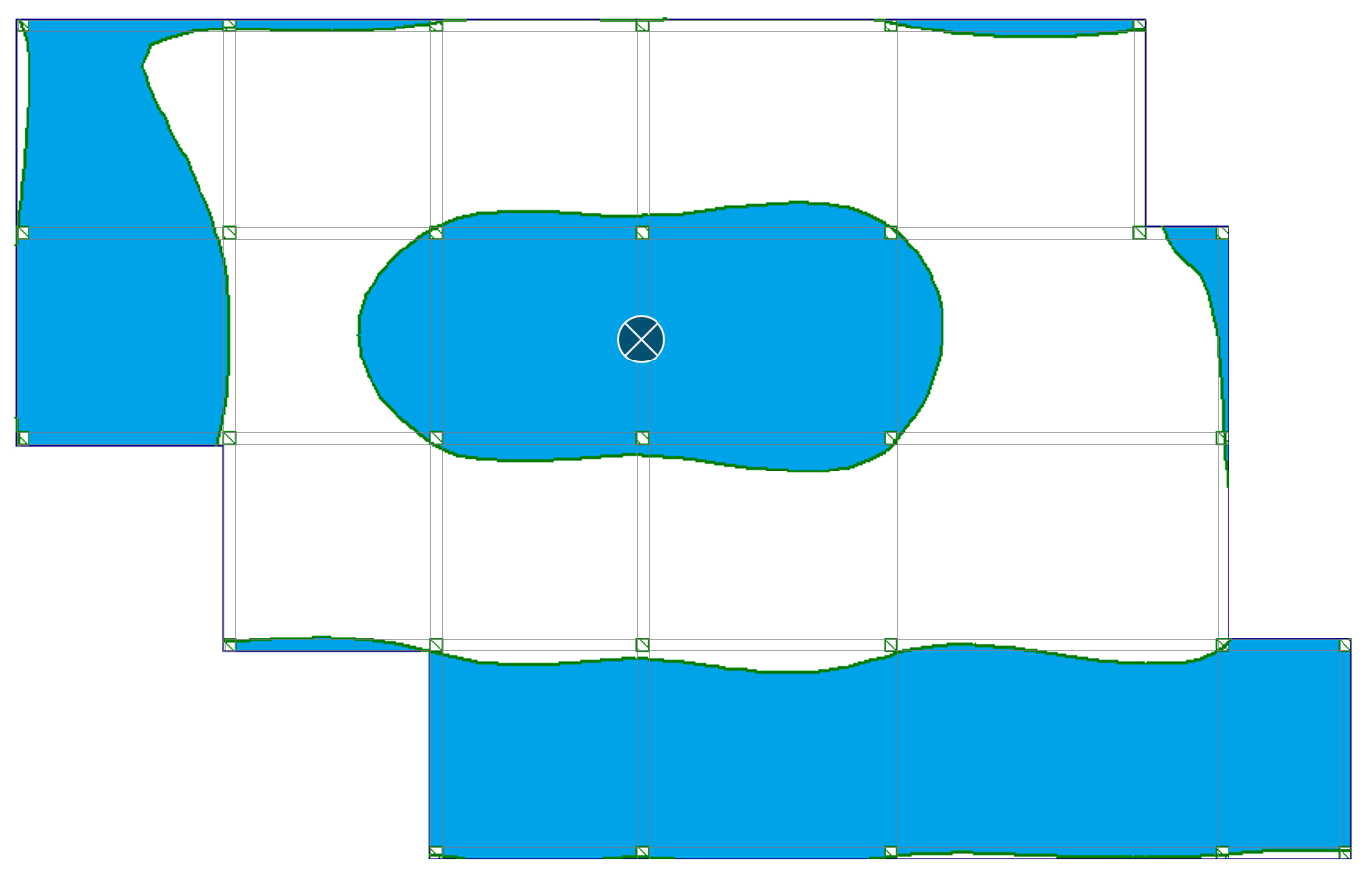 |
| d) podpora wewnętrzna (moment podporowy MY i reakcja RZ) | 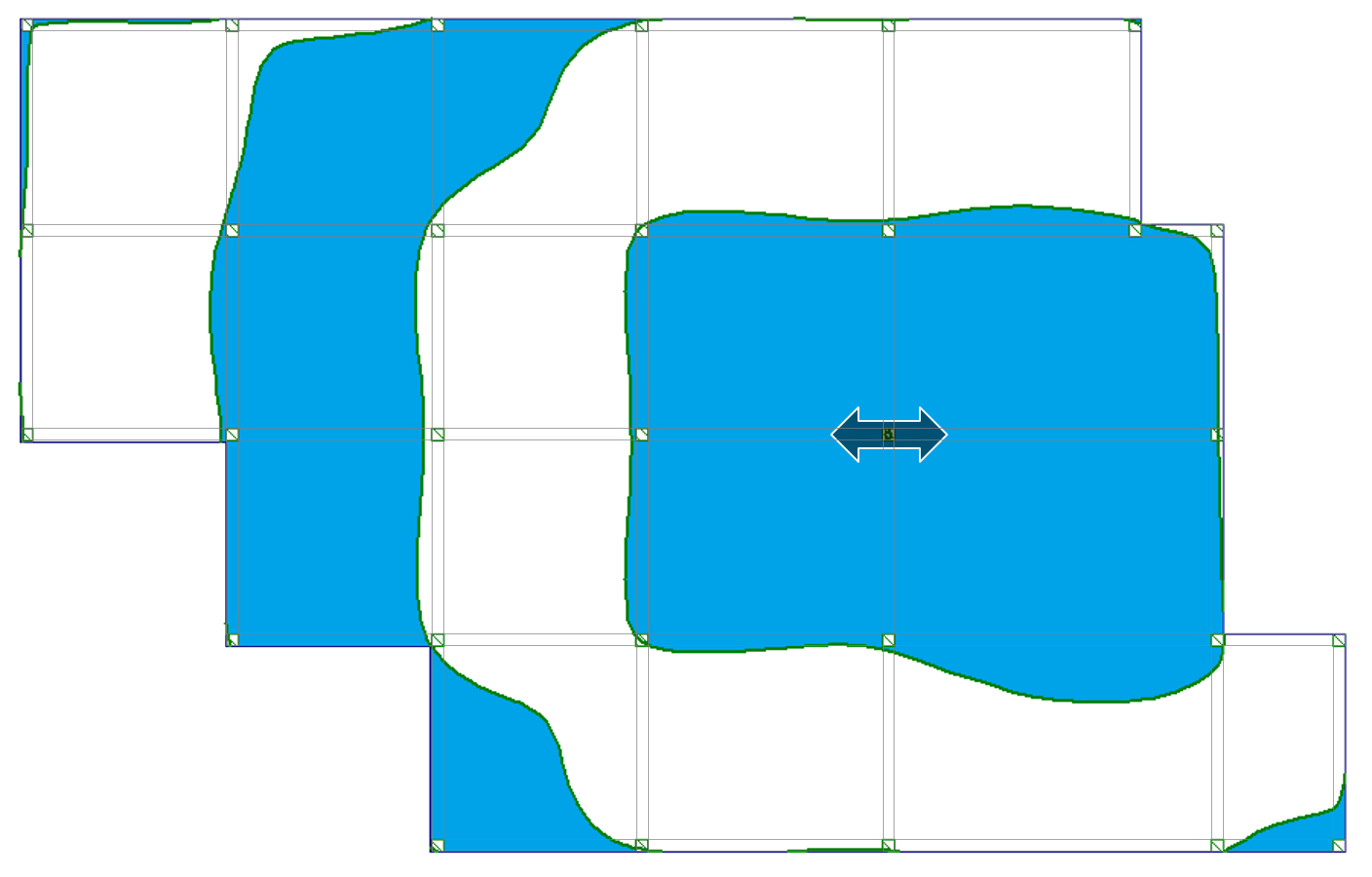 |
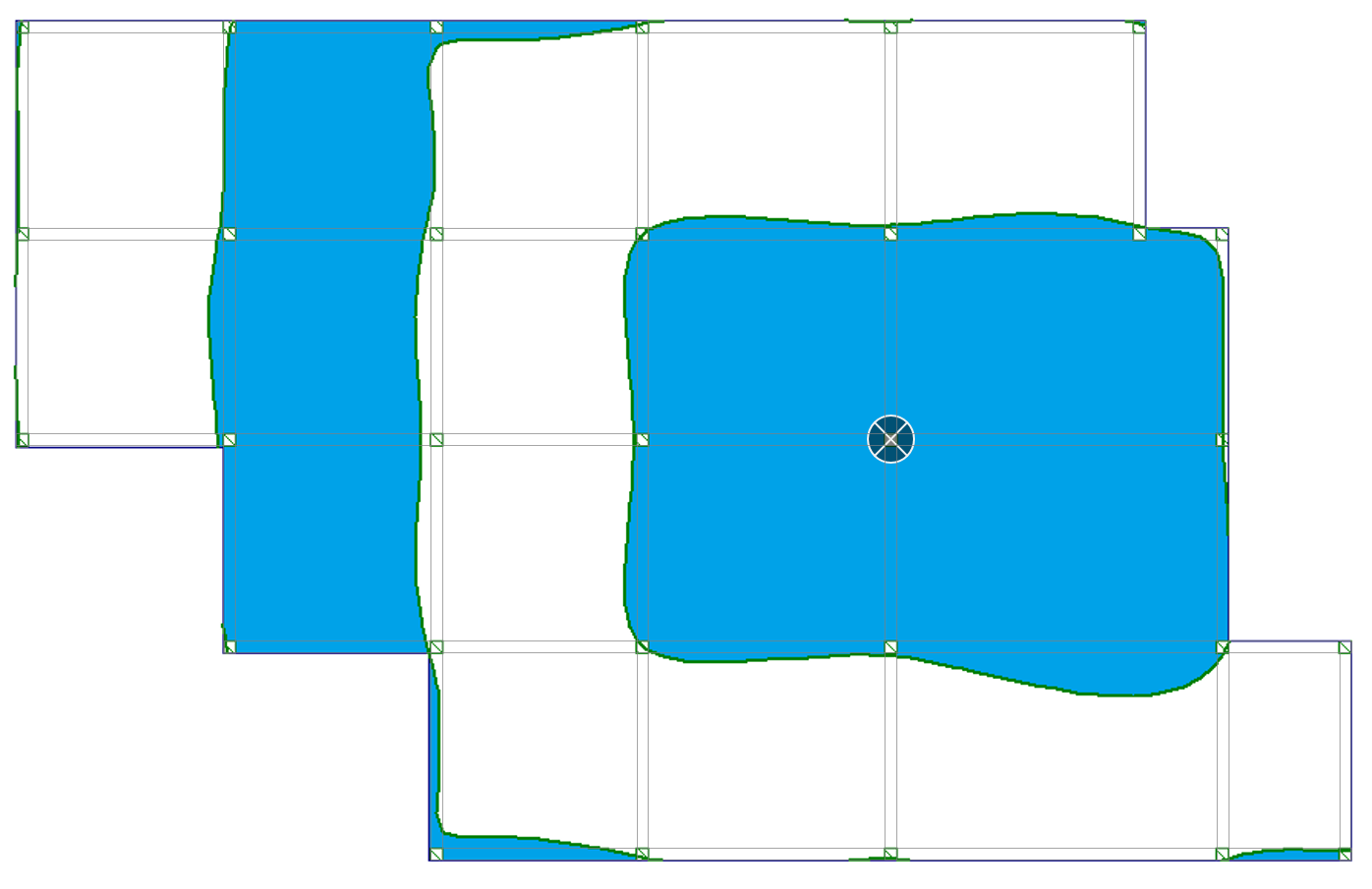 |
Zauważyłeś, że powierzchnie wpływu przebiegają krzywoliniowo przez poszczególne przęsła? Krzywe te pokrywają tylko część powierzchni poszczególnych pól stropu. Oznacza to, że niektóre obszary obciążenia zmiennego w przęśle działają odciążająco na analizowane wartości ugięć i momentów zginających.
Metody rozkładu obciążeń zmiennych
OK, wiemy jak wygląda rozwiązanie dokładne, jest ono jednak bardzo pracochłonne i najlepiej znaleźć inny, prostszy sposób na rozkład obciążeń zmiennych na stropie. Warunek podstawowy jest taki, żeby dokładność wyników była zbliżona do rozwiązania dokładnego.
W praktyce znane jest kilka sposobów rozkładu obciążeń zmiennych na stropach. Najczęściej stosowanymi metodami są m.in.:
- Schemat obciążeń niezależnych – polega na obciążeniu każdego pola jako osobny przypadek obciążenia,
- Schemat szachownicowy – tradycyjny sposób rozkładu obciążeń na wzór planszy szachownicy: jedno pole obciążone rozdzielone jednym polem nieobciążonym,
- Schemat pasmowy analogia do metody ram zastępczych – obciążenie ustawiane jest w pasmach przez cały strop w danym kierunku. Stosowany jest najczęściej przy stropach płytowo-słupowych, ale niektórzy wykorzystują to i w stropach belkowych,
- Schemat obciążenia ze współczynnikiem zwiększającym – rozłożenie obciążenia w ramach jednego przypadku obciążenia na całej powierzchni stropu zwiększonego o globalny współczynnik > 1.0,
- Schemat rozkładu obciążeń co 2. pole – alternatywny sposób polegający na obciążeniu co drugiego pola stropu w obu kierunkach w ramach jednego przypadku obciążenia (redukcja przypadków obciążenia do 4). Więcej o nim znajdziesz tutaj.
- Schemat rozkładu obciążeń co 3. pole – alternatywny sposób podobny do powyższego z tą różnicą, że obciążenie rozkłada się co trzecie pole stropu w obu kierunkach w ramach jednego przypadku obciążenia (redukcja przypadków obciążenia do 9). Więcej o nim znajdziesz tutaj.
Dla każdego z tych schematów przeprowadzę analizę sposobu rozkładu obciążeń zmiennych dla czterech wybranych miejsc stropu:
- a) przęsło wewnętrzne,
- b) przęsło skrajne,
- c) w linii podpór (w płycie nad belką) oraz
- d) podpora.
Pozwoli to porównać nam wyniki i ustalić, który schemat rozkładu obciążeń jest najbardziej efektywny i czy daje on wyniki zbliżone do rozwiązania dokładnego.
0. Rozkład obciążeń według powierzchni wpływu
Na początek zebrałem wyniki obliczeń dla momentów zginających i ugięć stropu uzyskane z powierzchni wpływu. W tabeli 2a i 2b zestawiłem wyniki dla tego rozwiązania. Opis tego jak to zrobić znajdziesz we wcześniejszym wpisie. Dla czytelności powtórzyłem tutaj rysunki z powierzchni wpływu z tab. 1.
Tab. 2a Wyniki momentów zginających dla rozkładu obciążeń wg powierzchni wpływu
| Rozpatrywane miejsce | Schemat obciążenia | Moment mX [kNm/m] |
|---|---|---|
| a) przęsło wewnętrzne |  |
+6.22 |
| b) przęsło skrajne |  |
+9.83 |
| c) linia podpór (nad belką) |  |
-7.55 |
| d) podpora wewnętrzna |  |
MY = -15.48 kNm |
Tab. 2b Wyniki ugięć dla rozkładu obciążeń wg powierzchni wpływu
| Rozpatrywane miejsce | Schemat obciążenia | Ugięcie [mm] |
|---|---|---|
| a) przęsło wewnętrzne |  |
-0.98 |
| b) przęsło skrajne |  |
-2.41 |
| c) linia podpór (nad belką) |  |
-0.46 |
| d) podpora wewnętrzna |  |
RZ = +220.3 |
Uwaga: Przyjąłem następującą konwencję oznaczeń: wartość mX dotyczy momentu zginającego oś X (poziomą), natomiast wartość MY dotyczy momentu podporowego (ujęcie wektorowe), RZ – reakcja podporowa.
1. Schemat obciążeń niezależnych
Tab. 3a Wyniki momentów zginających dla dla niezależnego rozkładu obciążeń
| Rozpatrywane miejsce | Schemat obciążenia | Moment mX [kNm/m] |
|---|---|---|
| a) przęsło wewnętrzne | 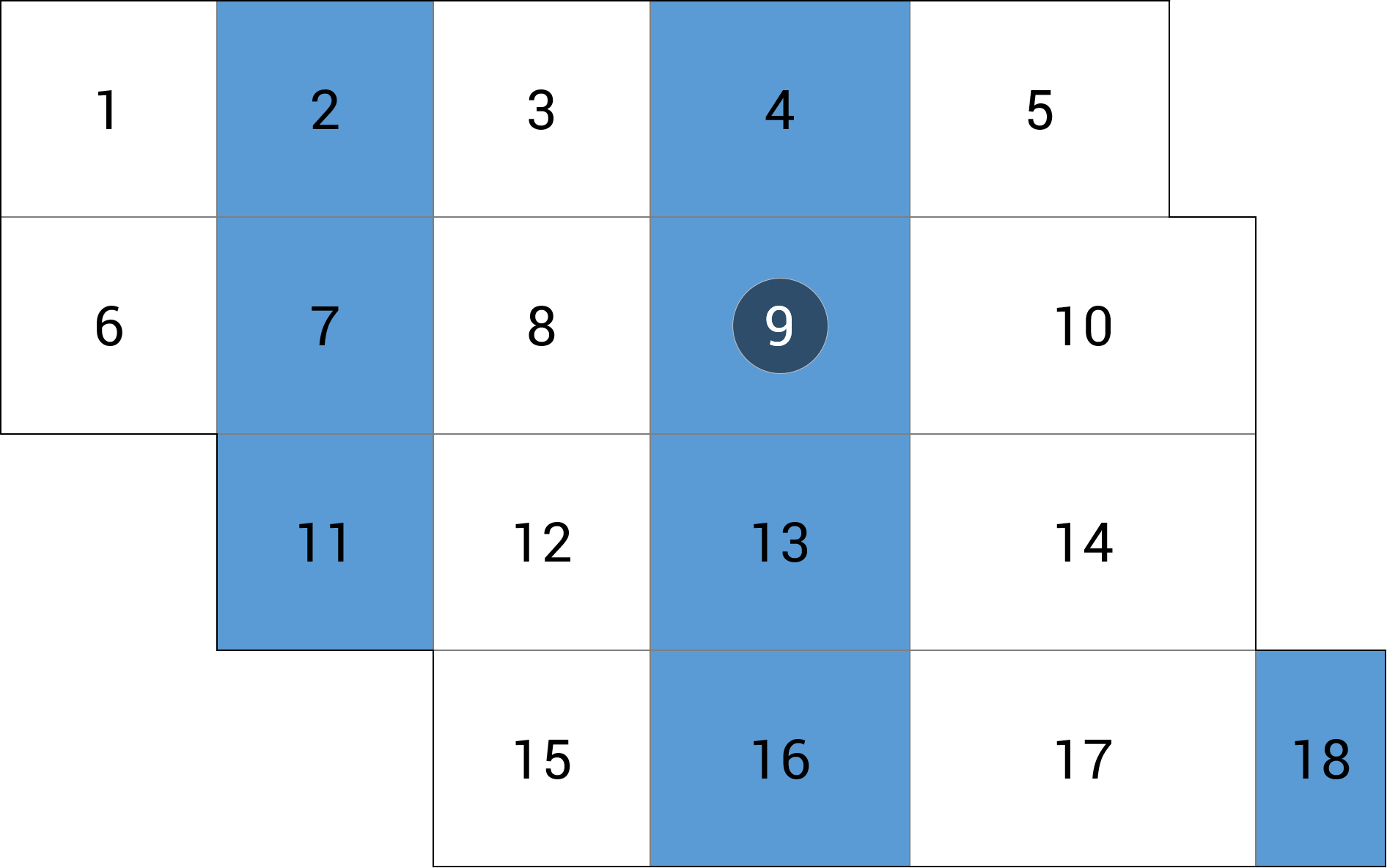 |
+6.25 (+0.5%) |
| b) przęsło skrajne | 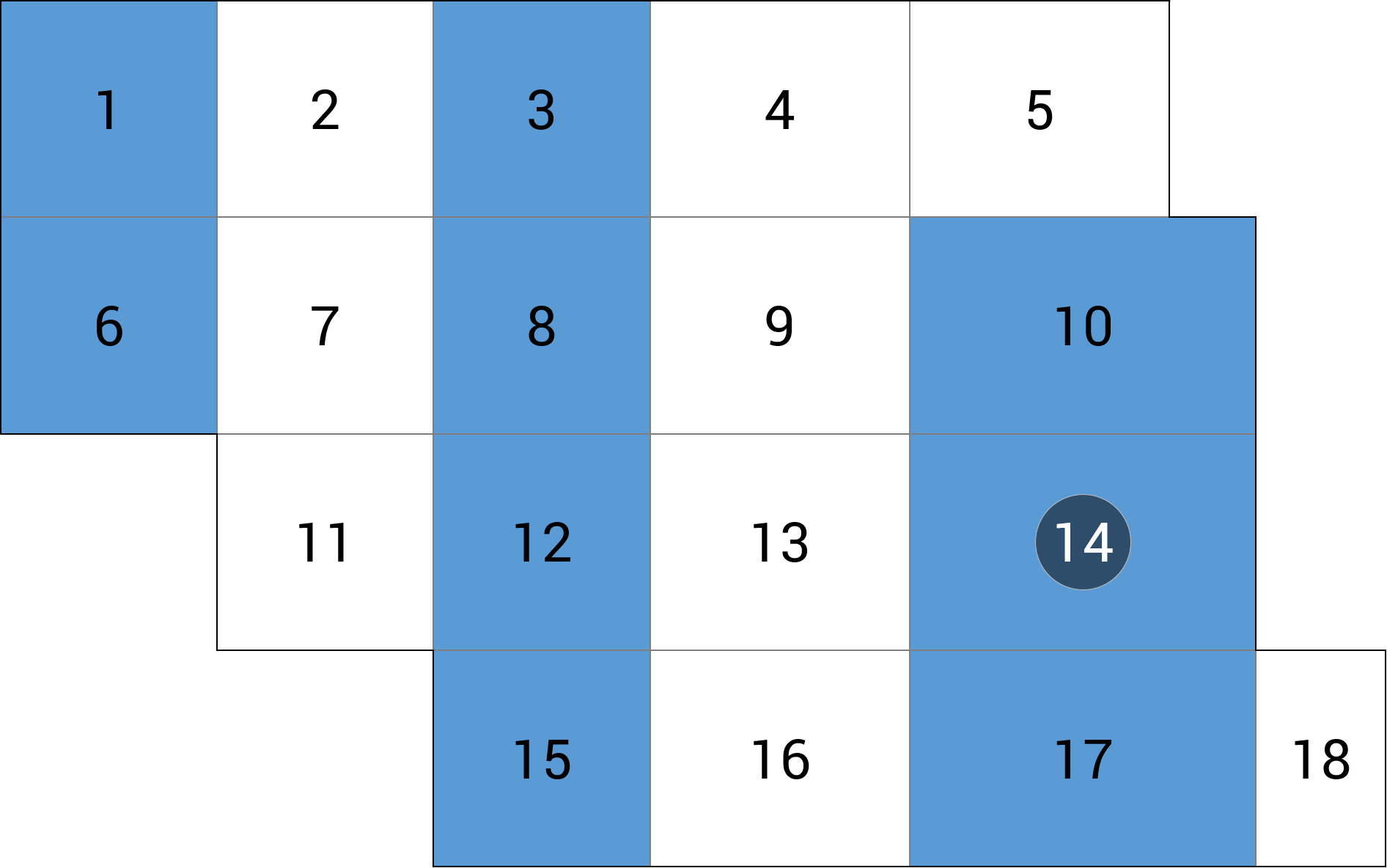 |
+9.85 (+0.2%) |
| c) linia podpór | 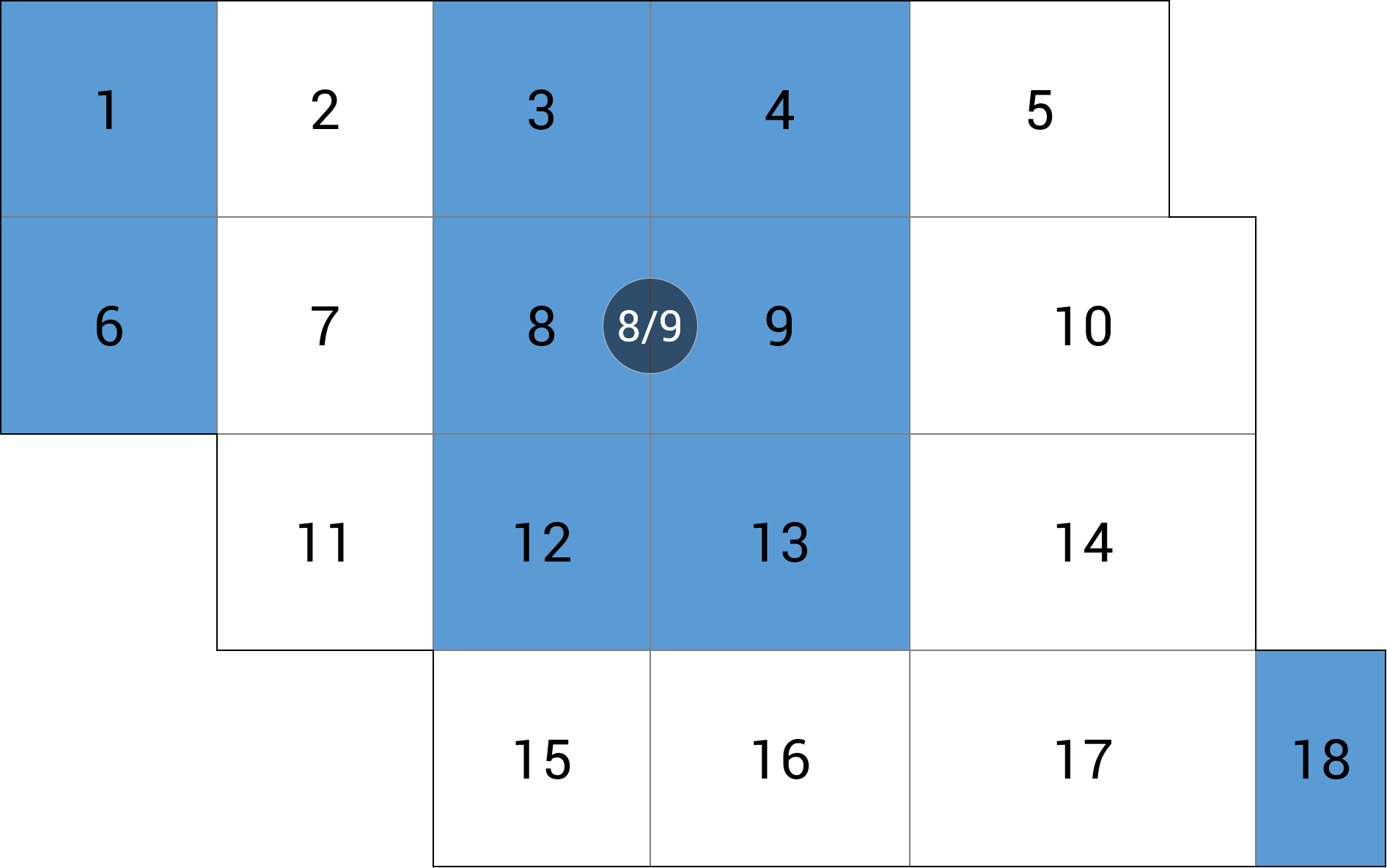 |
-6.74 (-10.7%) |
| d) podpora wewnętrzna | 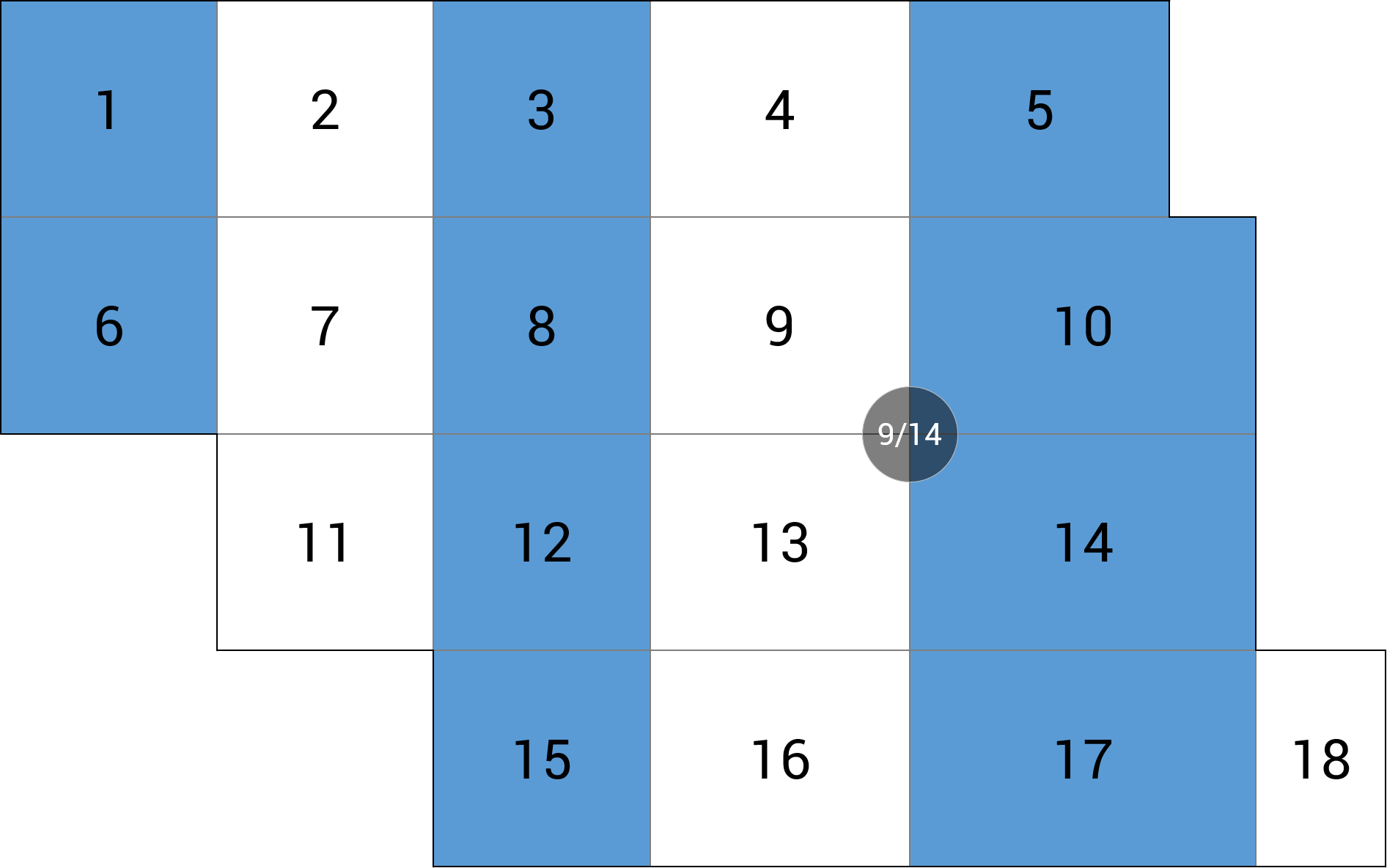 |
MY = -15.59 kNm (+0.7%) |
Tab. 3b Wyniki ugięć dla dla niezależnego rozkładu obciążeń
| Rozpatrywane miejsce | Schemat obciążenia | Ugięcie [mm] |
|---|---|---|
| a) przęsło wewnętrzne | (Jak dla mx) | -0.92 (-6.1%) |
| b) przęsło skrajne | (Jak dla mx) | -2.40 (-0.4%) |
| c) linia podpór | 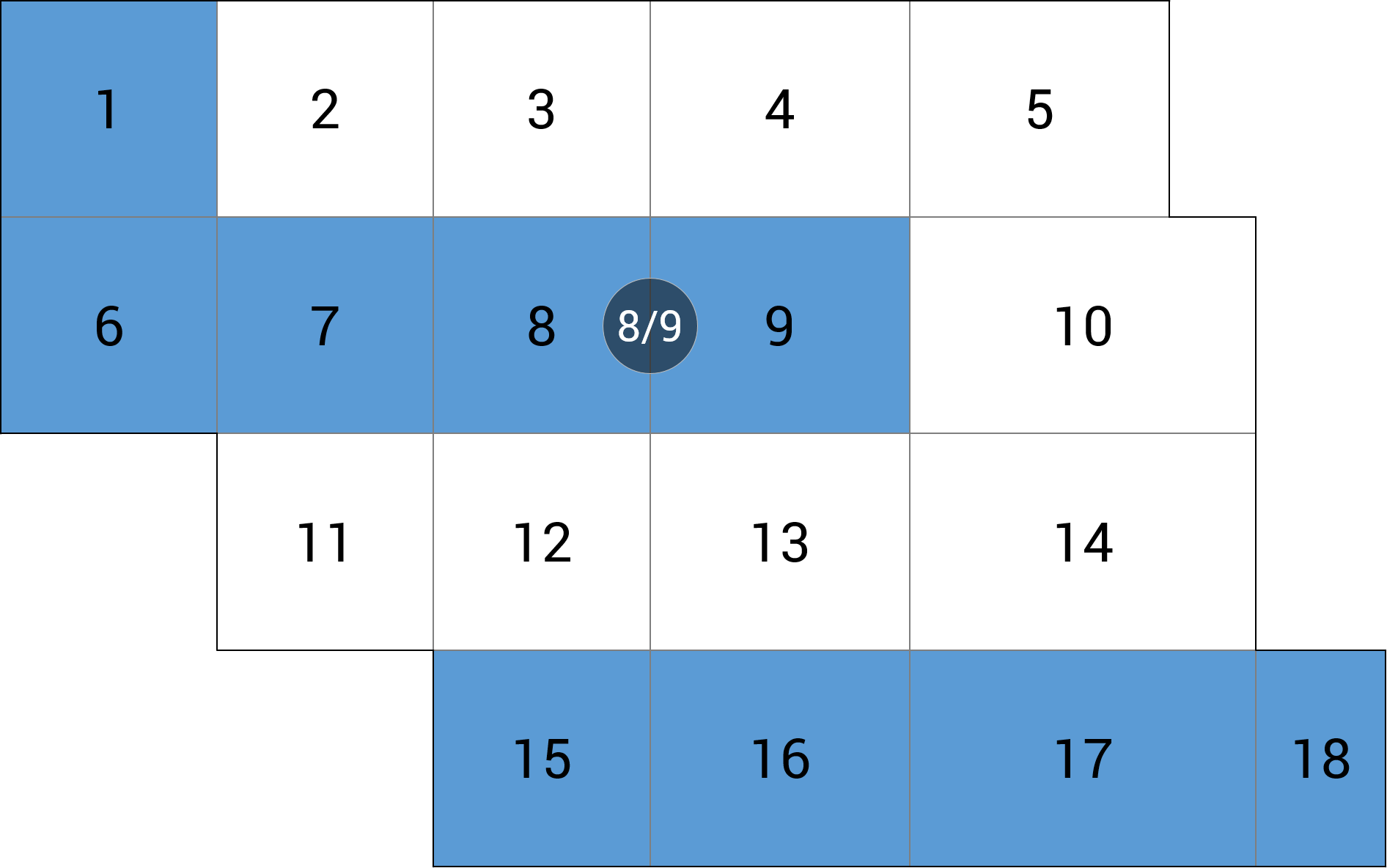 |
-0.46 (-0.0%) |
| d) podpora wewnętrzna | 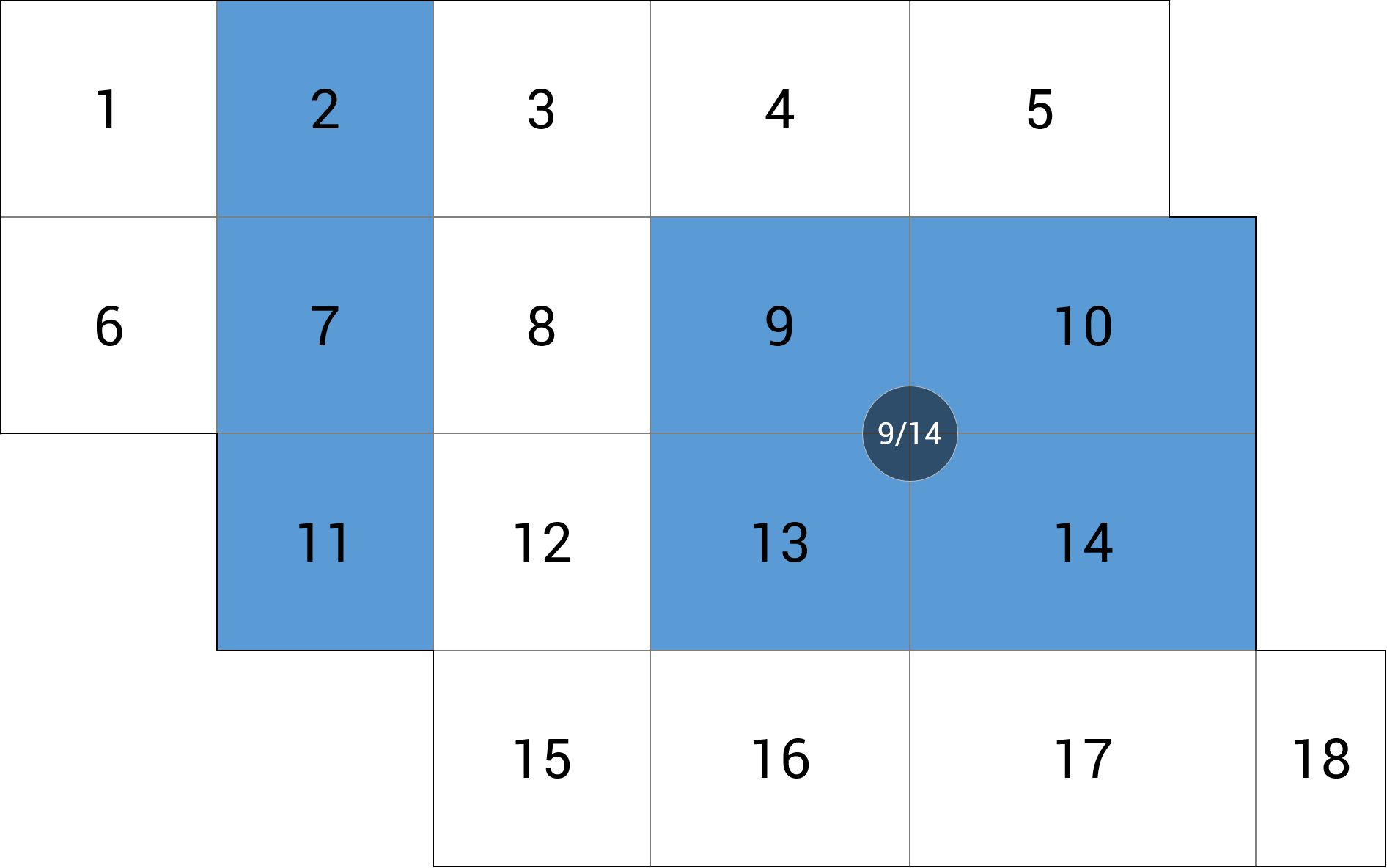 |
RZ = +219.3 kN (-0.5%) |
Uwaga techniczna: Wartości w nawiasach oznaczają błędy względne do rozwiązania dokładnego, tj. z powierzchni wpływu („+” oznacza przeszacowanie czyli zapas, „-” niedoszacowanie).
2. Schemat szachownicowy
Tab. 4a Wyniki momentów zginających dla szachownicowego rozkładu obciążeń
| Rozpatrywane miejsce | Schemat obciążenia | Moment mX [kNm/m] |
|---|---|---|
| a) przęsło wewnętrzne |  |
+3.90 (-37.3%) |
| b) przęsło skrajne | 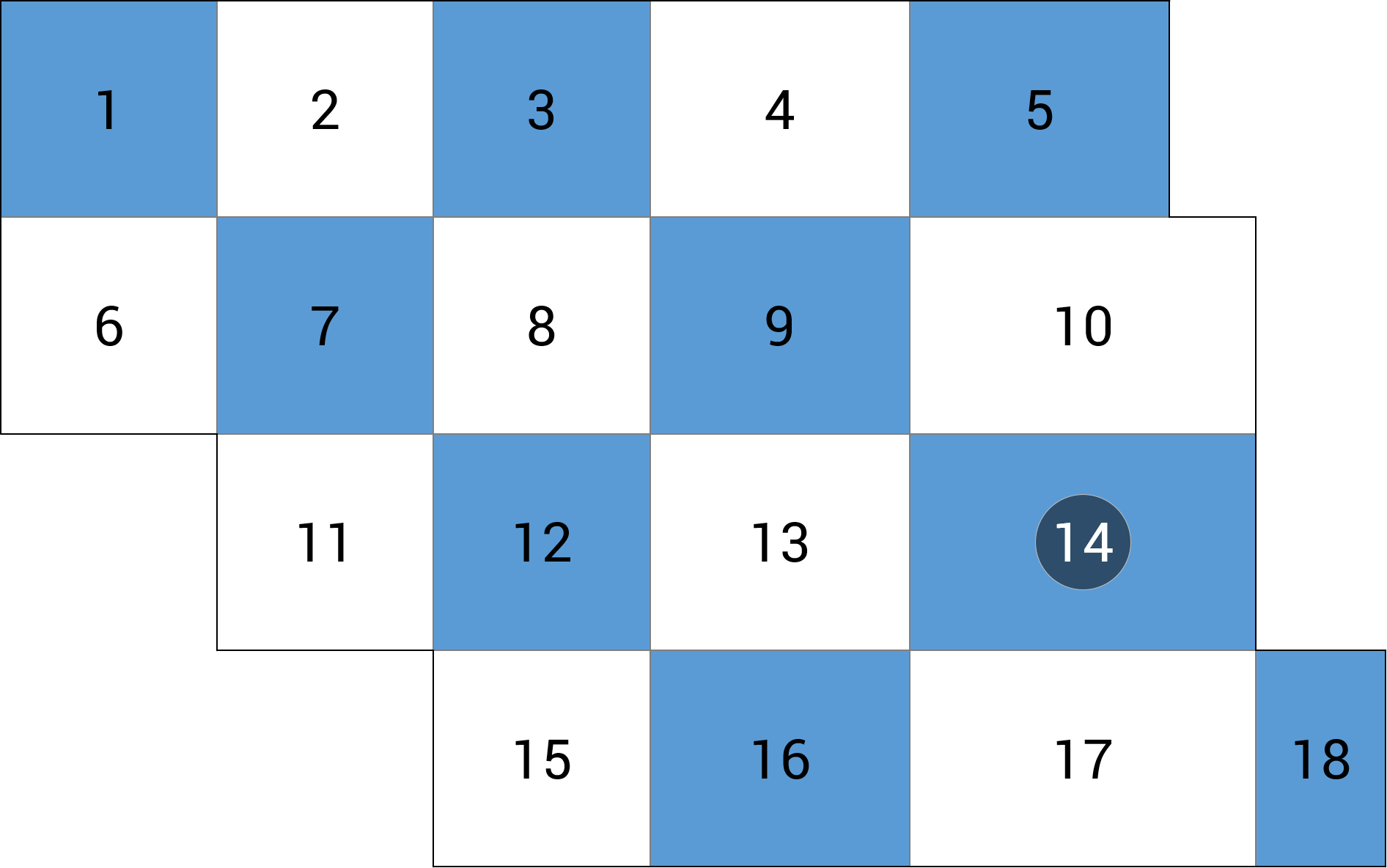 |
+6.56 (-33.3%) |
| c) linia podpór | 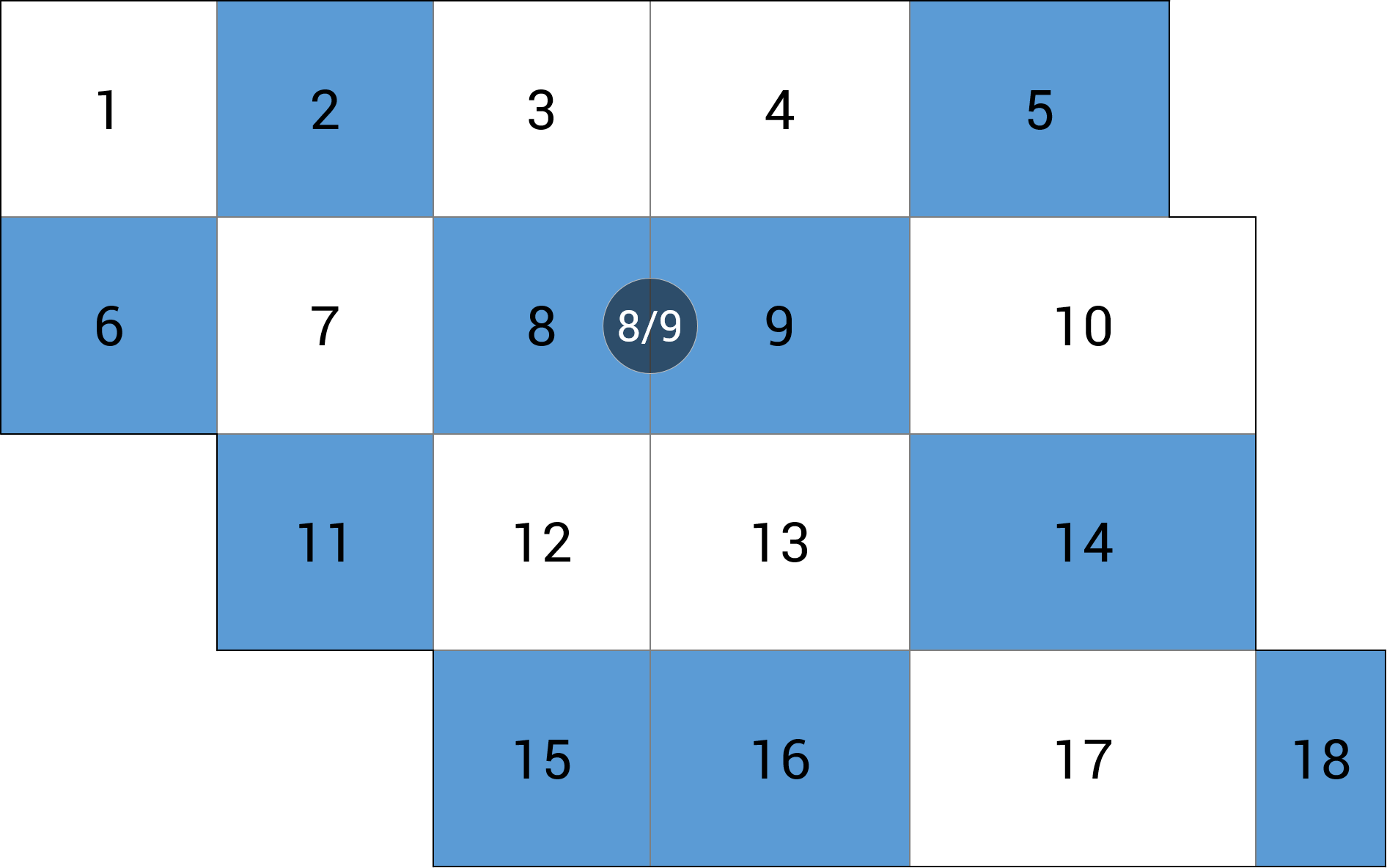 |
-3.97 (-47.4%) |
| d) podpora wewnętrzna | 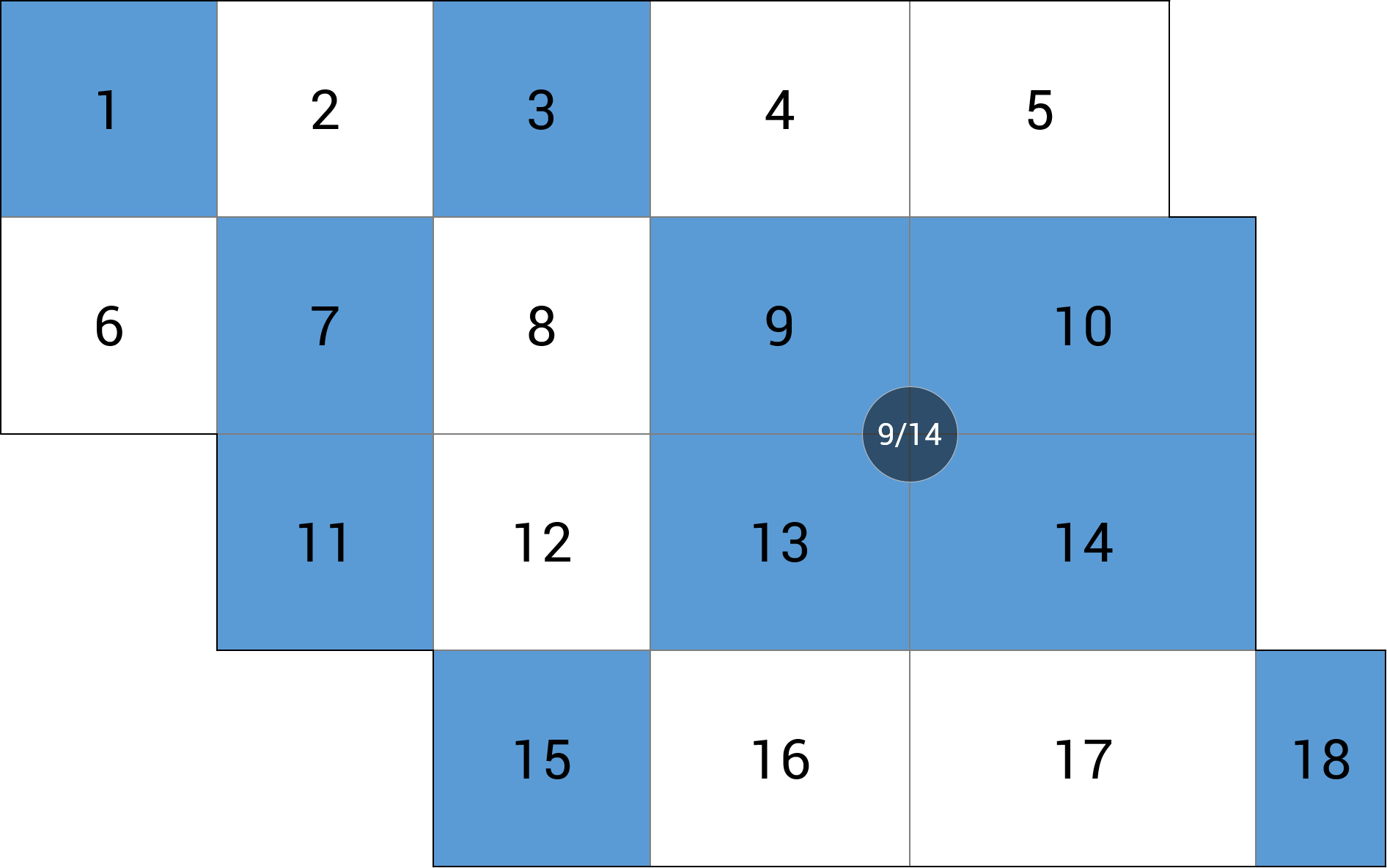 |
MY = -5.92 kNm (-61.8%) |
Tab. 4b Wyniki ugięć dla szachownicowego rozkładu obciążeń
| Rozpatrywane miejsce | Schemat obciążenia | Ugięcie [mm] |
|---|---|---|
| a) przęsło wewnętrzne | (Jak dla mx) | -0.48 (-51.0%) |
| b) przęsło skrajne | (Jak dla mx) | -1.45 (-39.8%) |
| c) linia podpór | (Jak dla mx) | -0.40 (-13.0%) |
| d) podpora wewnętrzna | (Jak dla MY) | RZ = +217.2 kN (-1.4%) |
3. Schemat pasmowy
Tab. 5a Wyniki momentów zginających dla pasmowego rozkładu obciążeń
| Rozpatrywane miejsce | Schemat obciążenia | Moment mX [kNm/m] |
|---|---|---|
| a) przęsło wewnętrzne | 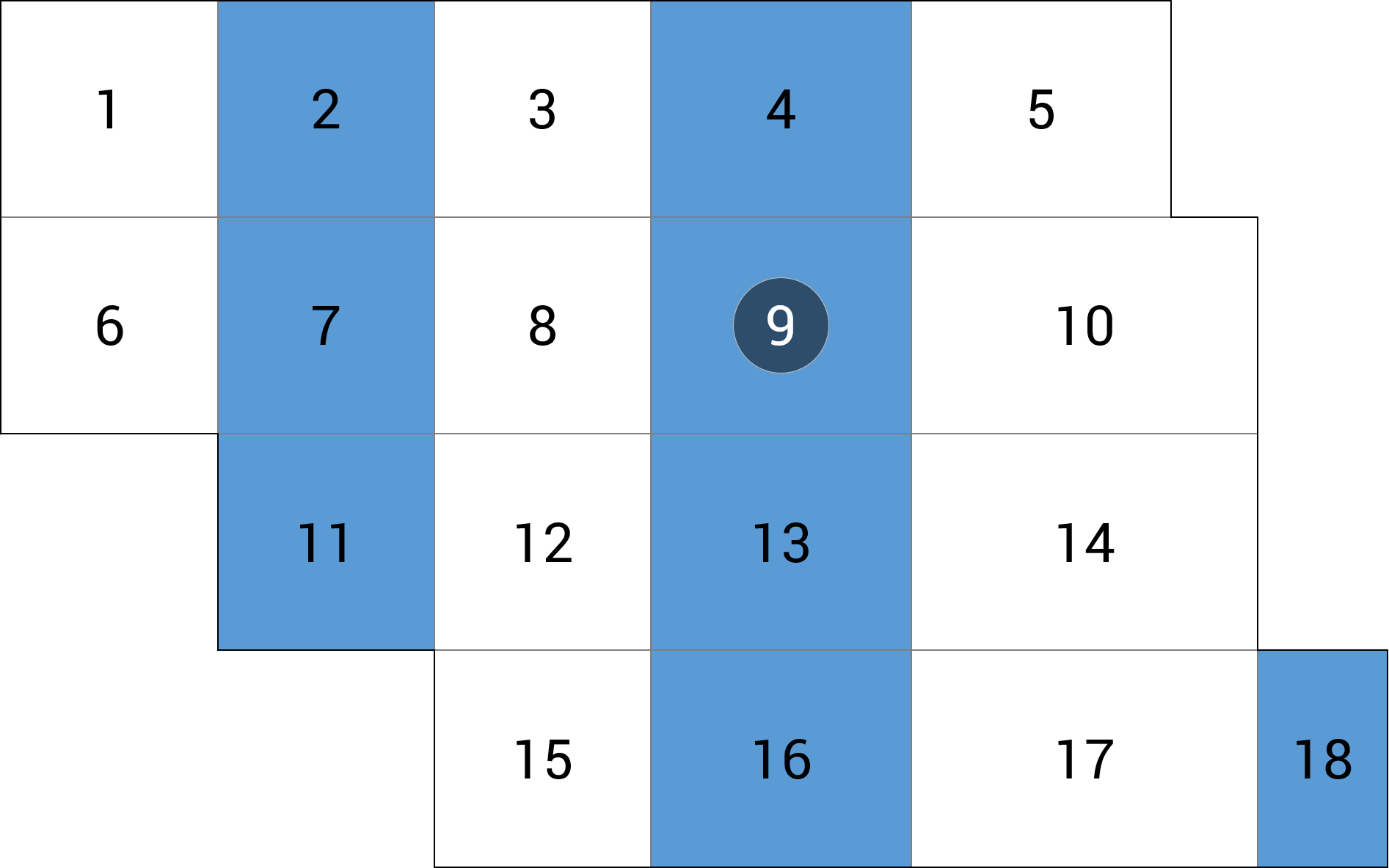 |
+6.24 (+0.3%) |
| b) przęsło skrajne | 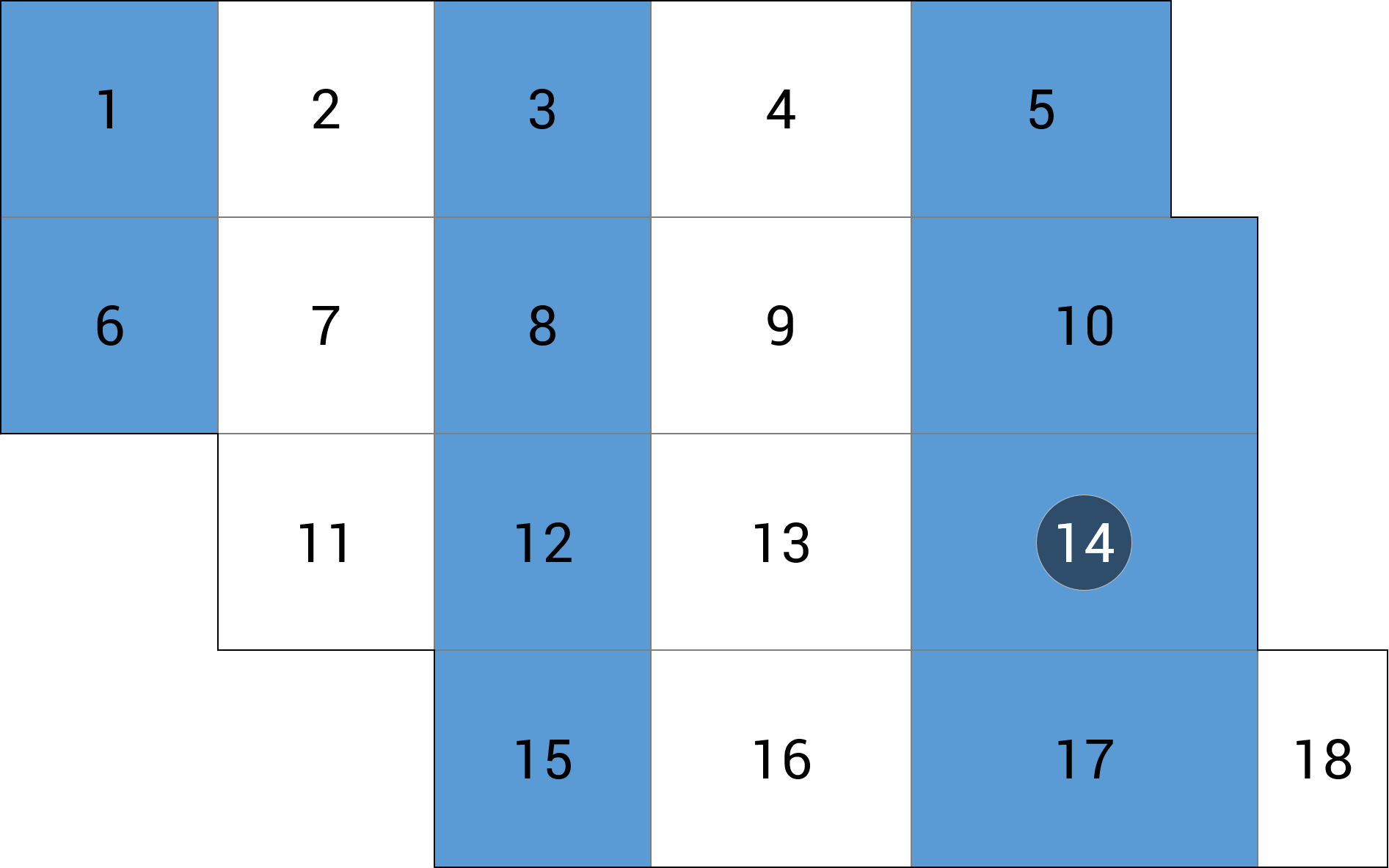 |
+9.81 (-0.2%) |
| c) linia podpór | 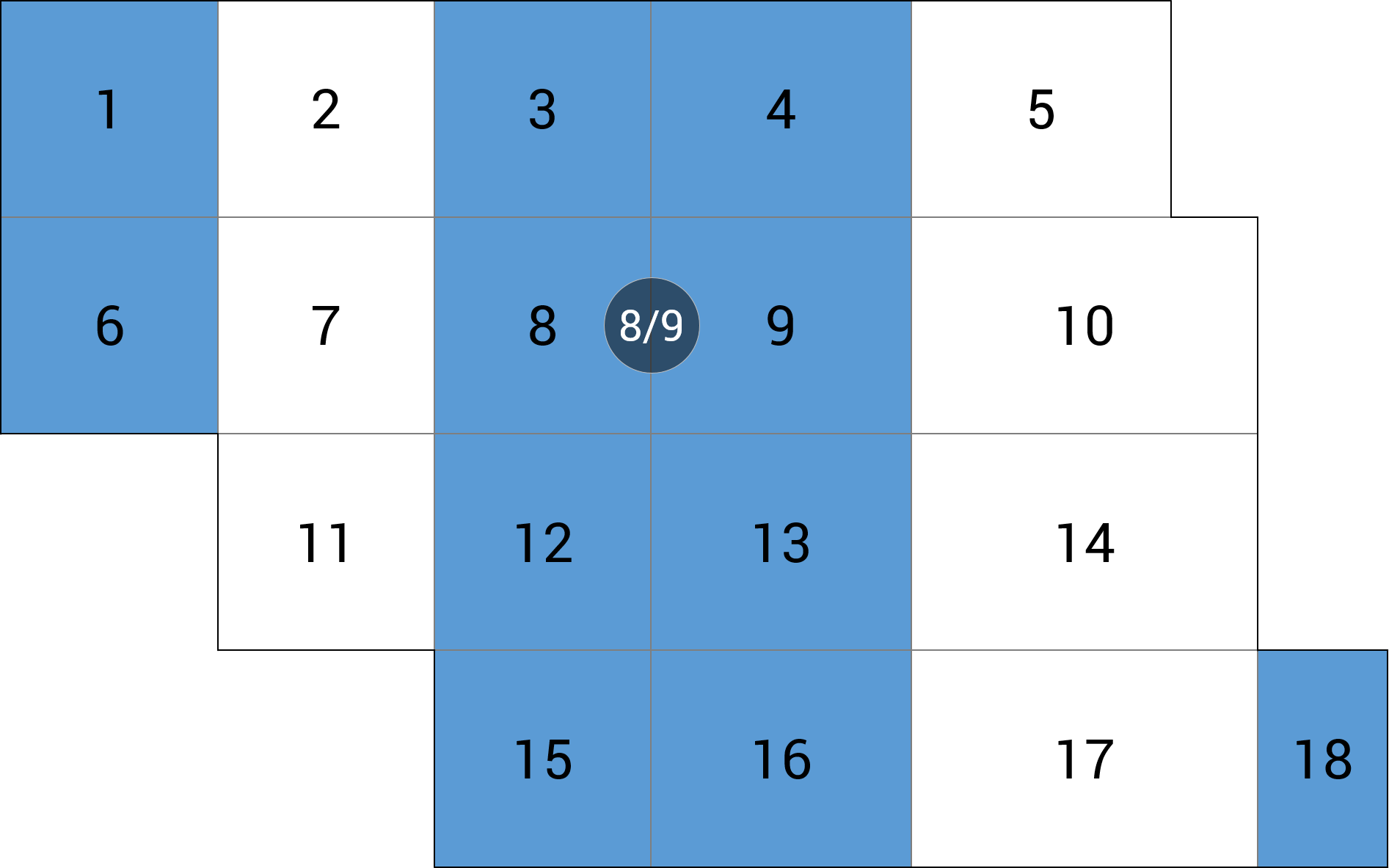 |
-6.66 (-11.8%) |
| d) podpora wewnętrzna |  |
MY = -5.88 kNm (-62.0%) |
Tab. 5b Wyniki ugięć dla pasmowego rozkładu obciążeń
| Rozpatrywane miejsce | Schemat obciążenia | Ugięcie [mm] |
|---|---|---|
| a) przęsło wewnętrzne | (Jak dla mx) | -0.92 (-6.1%) |
| b) przęsło skrajne | (Jak dla mx) | -2.39 (-0.8%) |
| c) linia podpór | (Jak dla mx) | -0.27 (-41.3%) |
| d) podpora wewnętrzna | (Jak dla MY) | RZ = +195.1 kN (-11.4%) |
4a. Obciążenie na całej powierzchni x Faktor = 1.20
Tab. 6a Wyniki momentów zginających dla obciążenia na całej powierzchni stropu x Faktor = 1.20
| Rozpatrywane miejsce | Schemat obciążenia | Moment mX [kNm/m] |
|---|---|---|
| a) przęsło wewnętrzne |  |
+3.95 (-36.5%) |
| b) przęsło skrajne | (Jak dla a)) | +10.34 (+5.2%) |
| c) linia podpór | (Jak dla a) | -6.05 (-19.9%) |
| d) podpora wewnętrzna | (Jak dla a)) | MY = -8.42 kNm (-45.6%) |
Tab. 6b Wyniki ugięć dla obciążenia na całej powierzchni stropu x Faktor = 1.20
| Rozpatrywane miejsce | Schemat obciążenia | Ugięcie [mm] |
|---|---|---|
| a) przęsło wewnętrzne | (Jak dla mx) | -0.45 (-54.1%) |
| b) przęsło skrajne | (Jak dla mx) | -2.02 (-16.2%) |
| c) linia podpór | (Jak dla mx) | -0.22 (-52.2%) |
| d) podpora wewnętrzna | (Jak dla MY) | RZ = 225.0 kN (+2.2%) |
4b. Obciążenie na całej powierzchni x Faktor = 1.30
Tab. 7a Wyniki momentów zginających dla obciążenia na całej powierzchni stropu x Faktor = 1.30
| Rozpatrywane miejsce | Schemat obciążenia | Moment mX [kNm/m] |
|---|---|---|
| a) przęsło wewnętrzne |  |
+4.27 (-31.4%) |
| b) przęsło skrajne | (Jak dla a)) | +11.21 (+14.0%) |
| c) linia podpór | (Jak dla a)) | -6.55 (-13.2%) |
| d) podpora wewnętrzna | (Jak dla a)) | MY = -9.12 kNm (-41.1%) |
Tab. 7b Wyniki ugięć dla obciążenia na całej powierzchni stropu x Faktor = 1.30
| Rozpatrywane miejsce | Schemat obciążenia | Ugięcie [mm] |
|---|---|---|
| a) przęsło wewnętrzne | (Jak dla mx) | -0.45 (-54.1%) |
| b) przęsło skrajne | (Jak dla mx) | -2.02 (-16.2%) |
| c) linia podpór | (Jak dla mx) | -0.22 (-52.2%) |
| d) podpora wewnętrzna | (Jak dla MY) | RZ = 243.8 kN (+10.7%) |

5. Schemat rozkładu obciążeń co 2. pole
Schemat co 2. pole i co 3. pole zaproponowałem w poprzednim wpisie jako alternatywę dla typowych schematów rozkładu obciążeń zmiennych. Schematy te wykorzystują zalety schematu niezależnego (por. pkt. 1).
Za cel postawiłem sobie zaproponowanie metody, która będzie (1) mniej pracochłonna od przedstawionych poprzednio metod tradycyjnych oraz (2) jej dokładność będzie zbliżona do tej otrzymanej z rozkładu obciążeń wg schematu niezależnego.
Tab. 8a Wyniki momentów zginających dla alternatywnego rozkładu obciążeń zmiennych co 2. pole
| Rozpatrywane miejsce | Schemat obciążenia | Moment mX [kNm/m] |
|---|---|---|
| a) przęsło wewnętrzne | 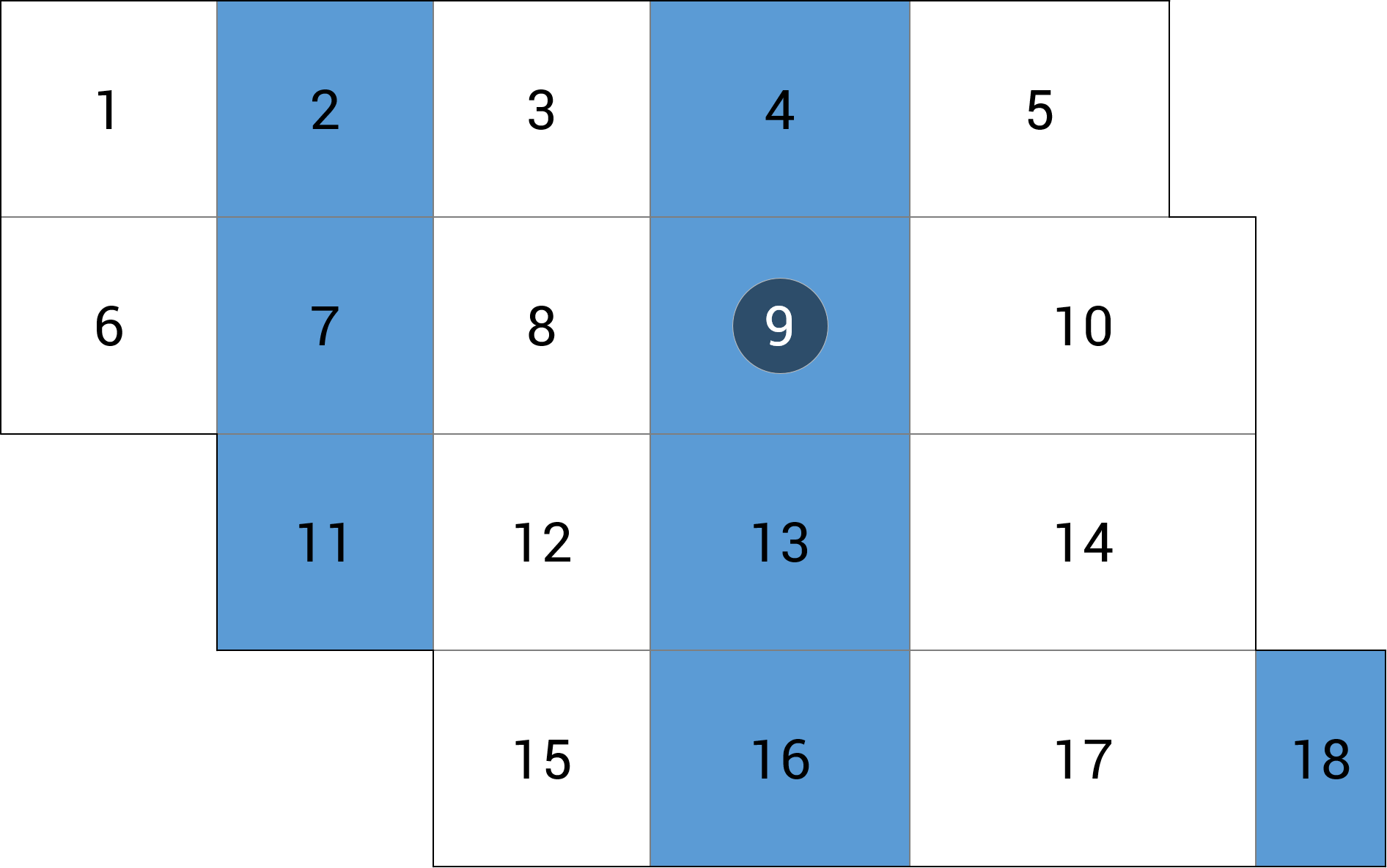 |
+6.25 (+0.5%) |
| b) przęsło skrajne | 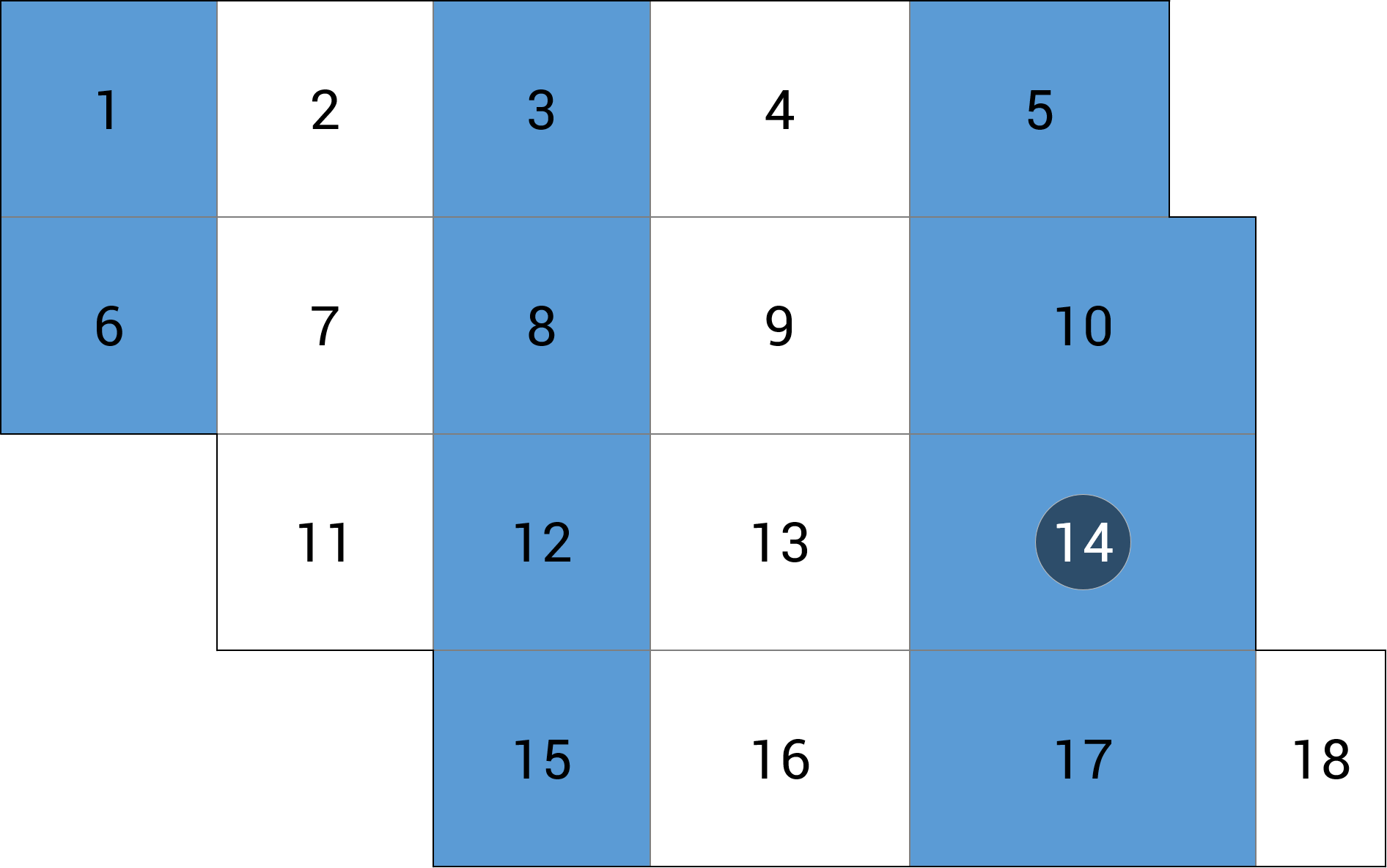 |
+9.81 (-0.2%) |
| c) linia podpór | 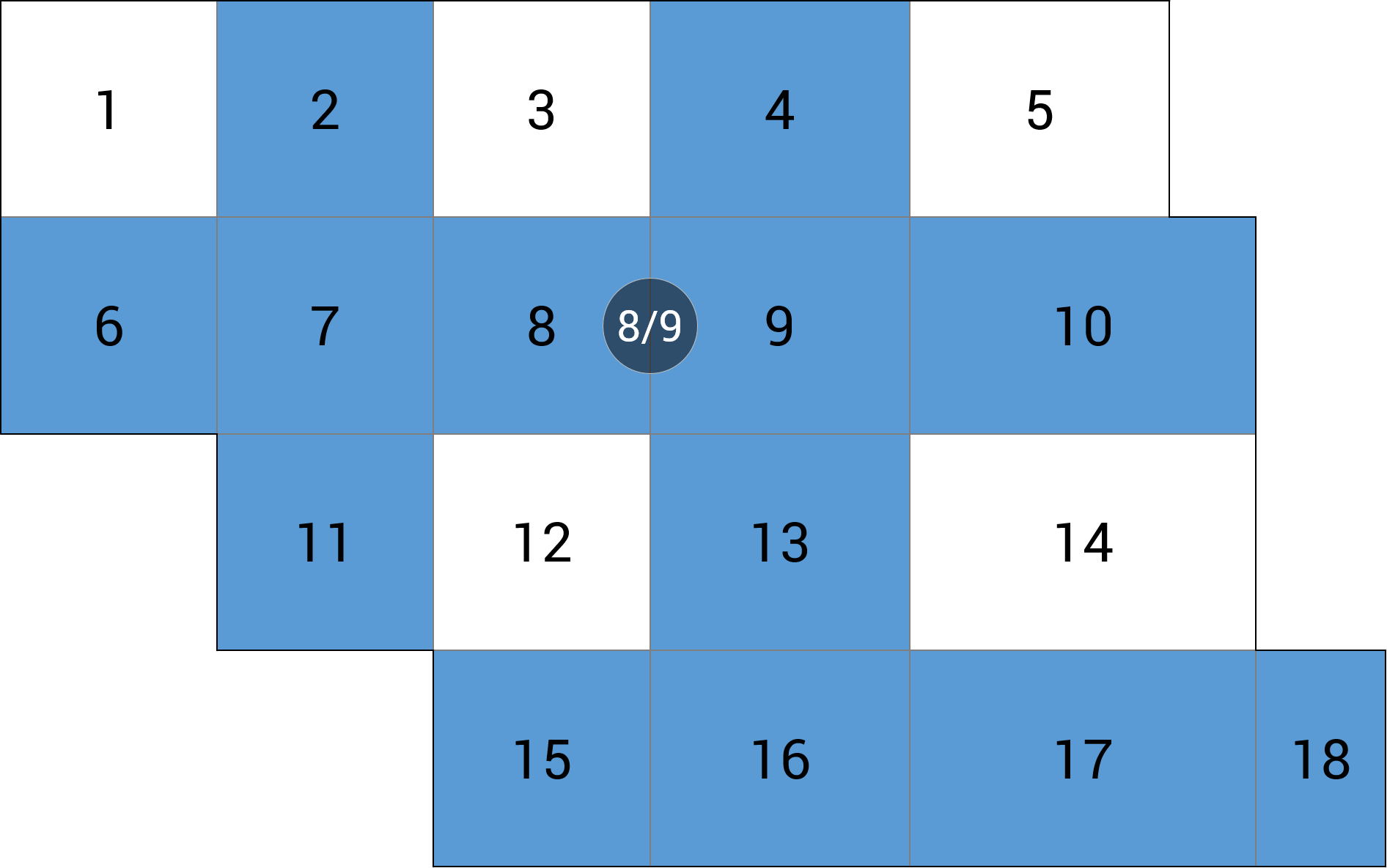 |
-5.37 (-28.9%) |
| d) podpora wewnętrzna | 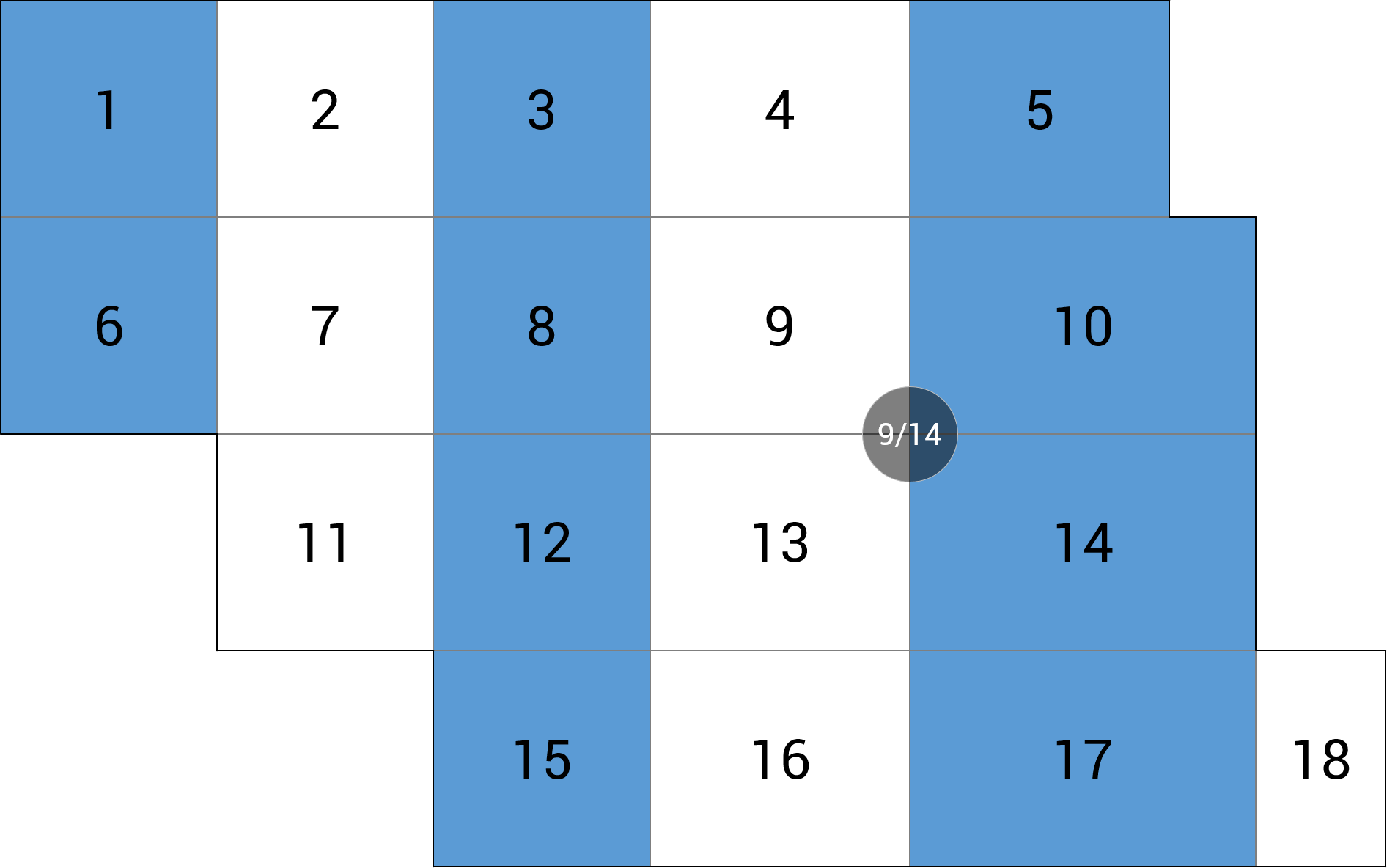 |
MY = -15.59 kNm (+0.7%) |
Tab. 8b Wyniki ugięć dla alternatywnego rozkładu obciążeń zmiennych co 2. pole
| Rozpatrywane miejsce | Schemat obciążenia | Ugięcie [mm] |
|---|---|---|
| a) przęsło wewnętrzne | (Jak dla mx) | -0.92 (-6.1%) |
| b) przęsło skrajne | (Jak dla mx) | -2.39 (-0.8%) |
| c) linia podpór | 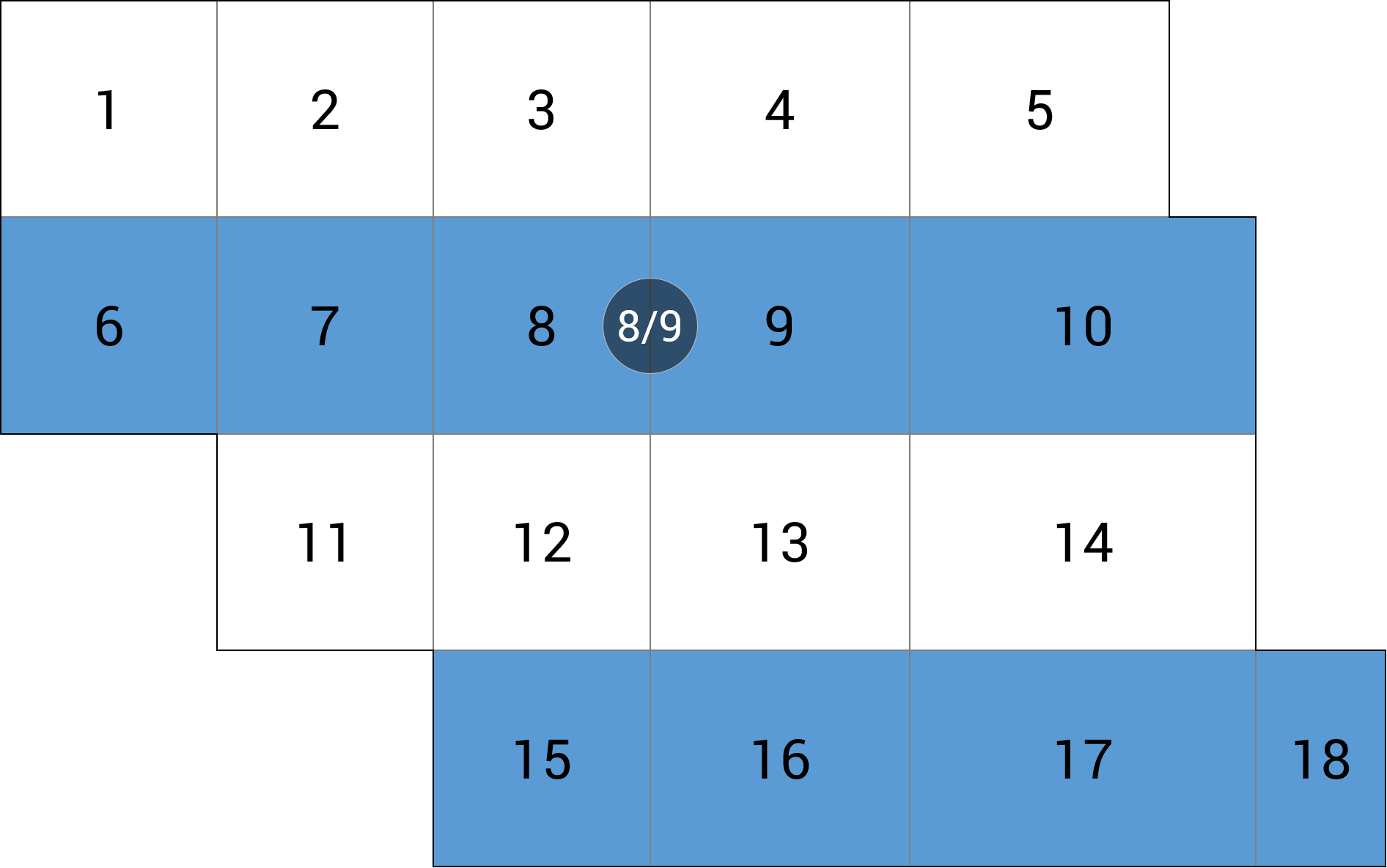 |
-0.44 (-4.3%) |
| d) podpora wewnętrzna |  |
RZ = +187.5 kN (-14.9%) |
6. Schemat rozkładu obciążeń co 3. pole
Tab. 9a Wyniki momentów zginających alternatywnego rozkładu obciążeń zmiennych co 3. pole
| Rozpatrywane miejsce | Schemat obciążenia | Moment mX [kNm/m] |
|---|---|---|
| a) przęsło wewnętrzne | 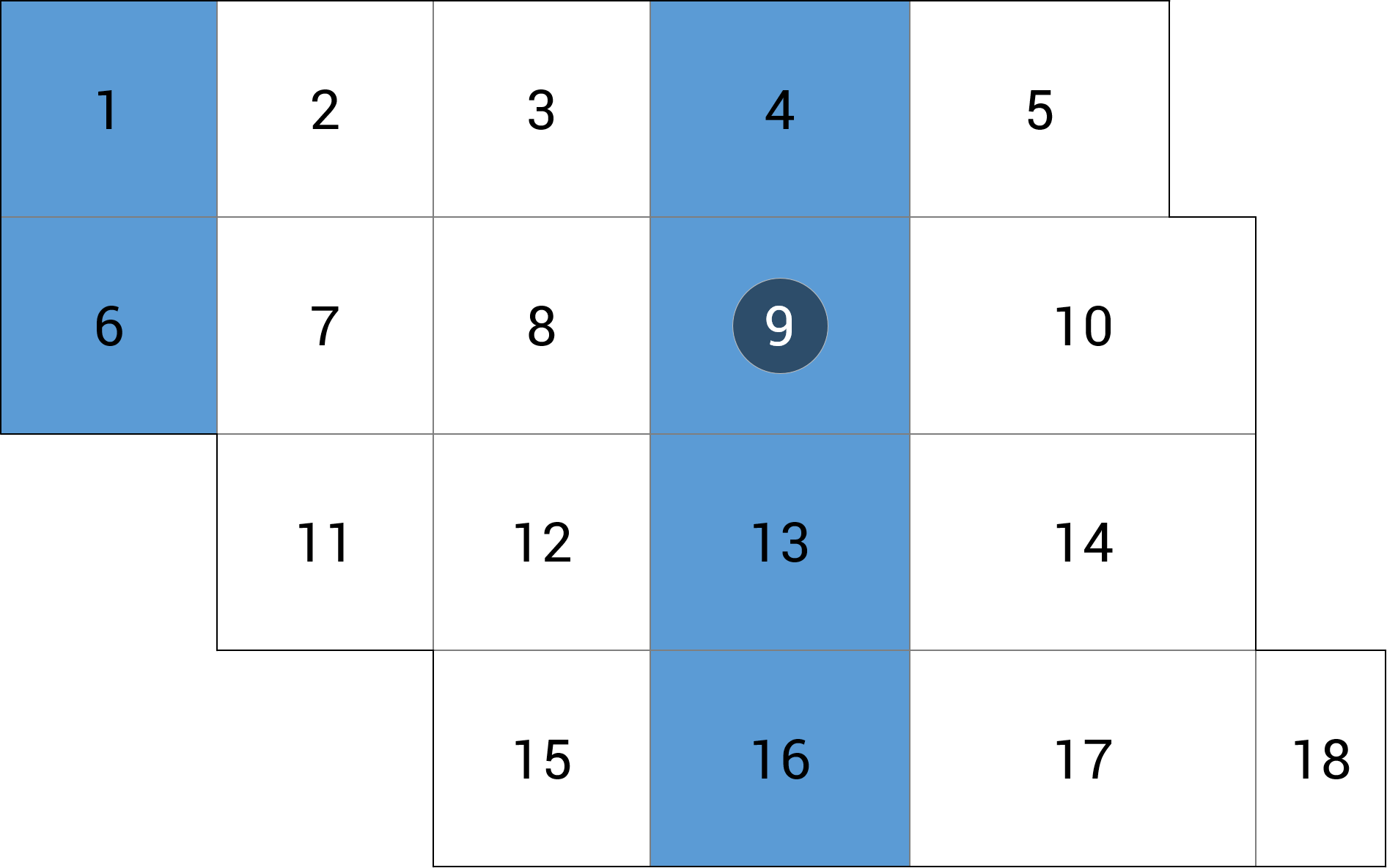 |
+6.05 (-2.7%) |
| b) przęsło skrajne | 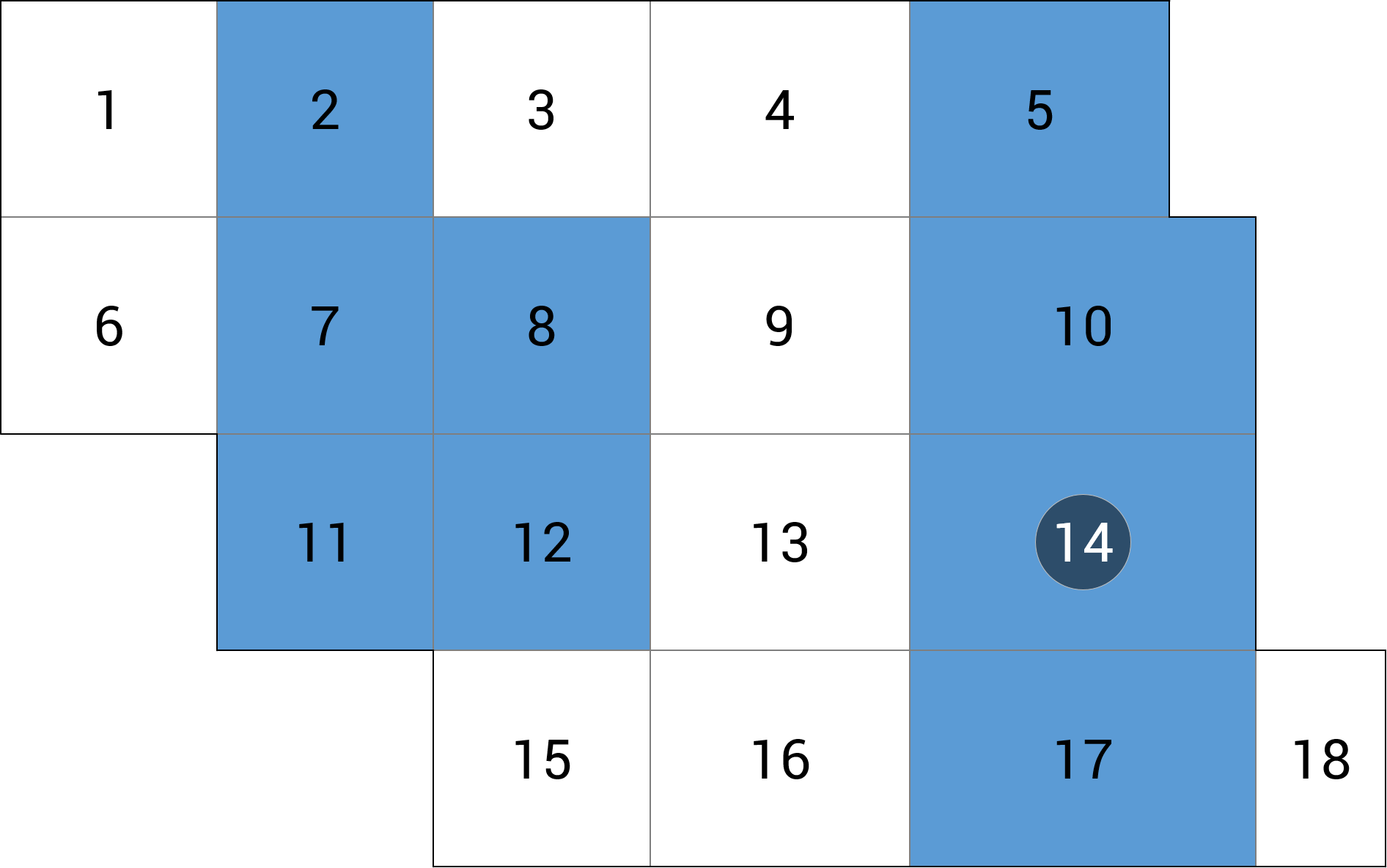 |
+9.74 (-0.9%) |
| c) linia podpór | 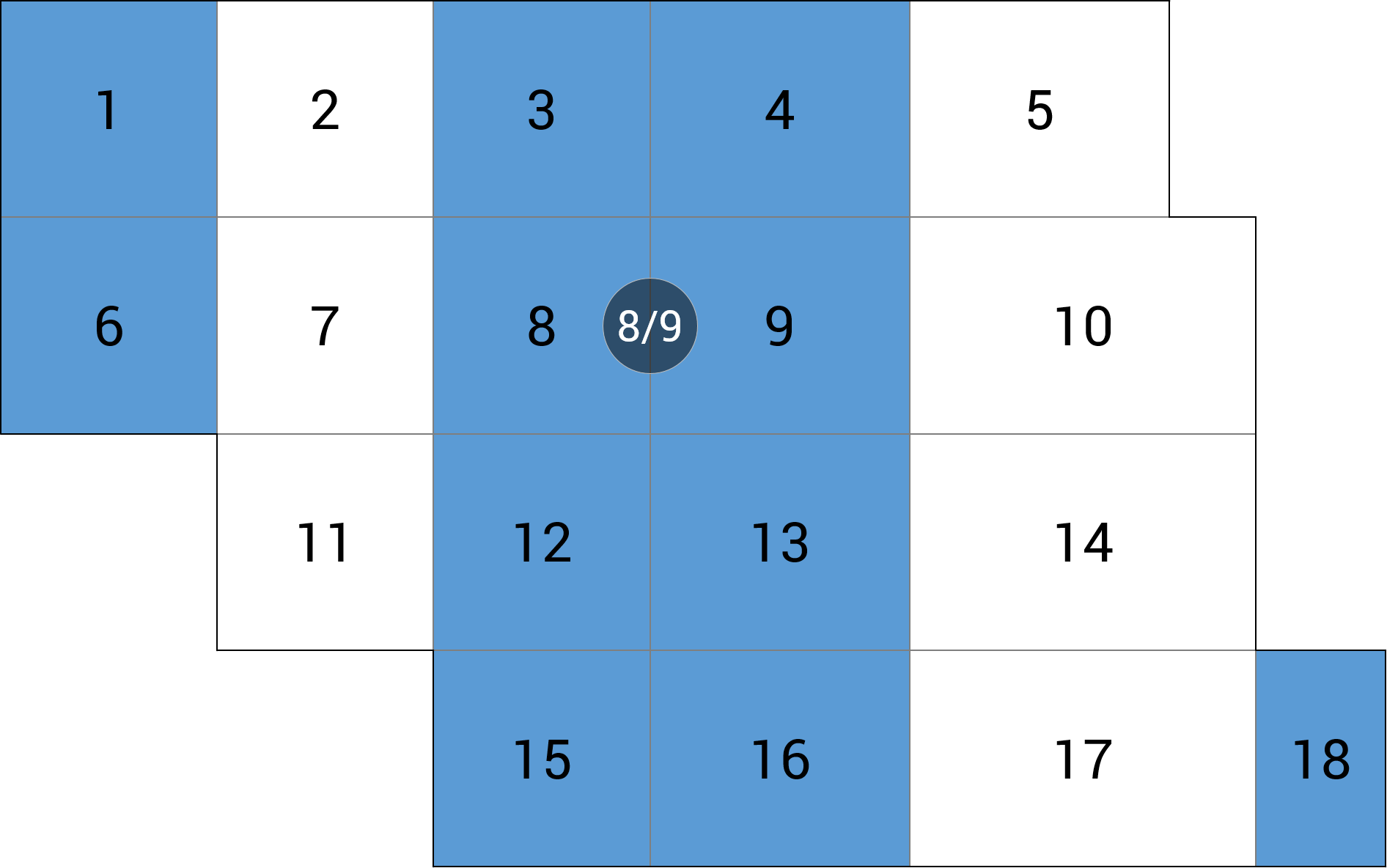 |
-6.66 (-11.8%) |
| d) podpora wewnętrzna | 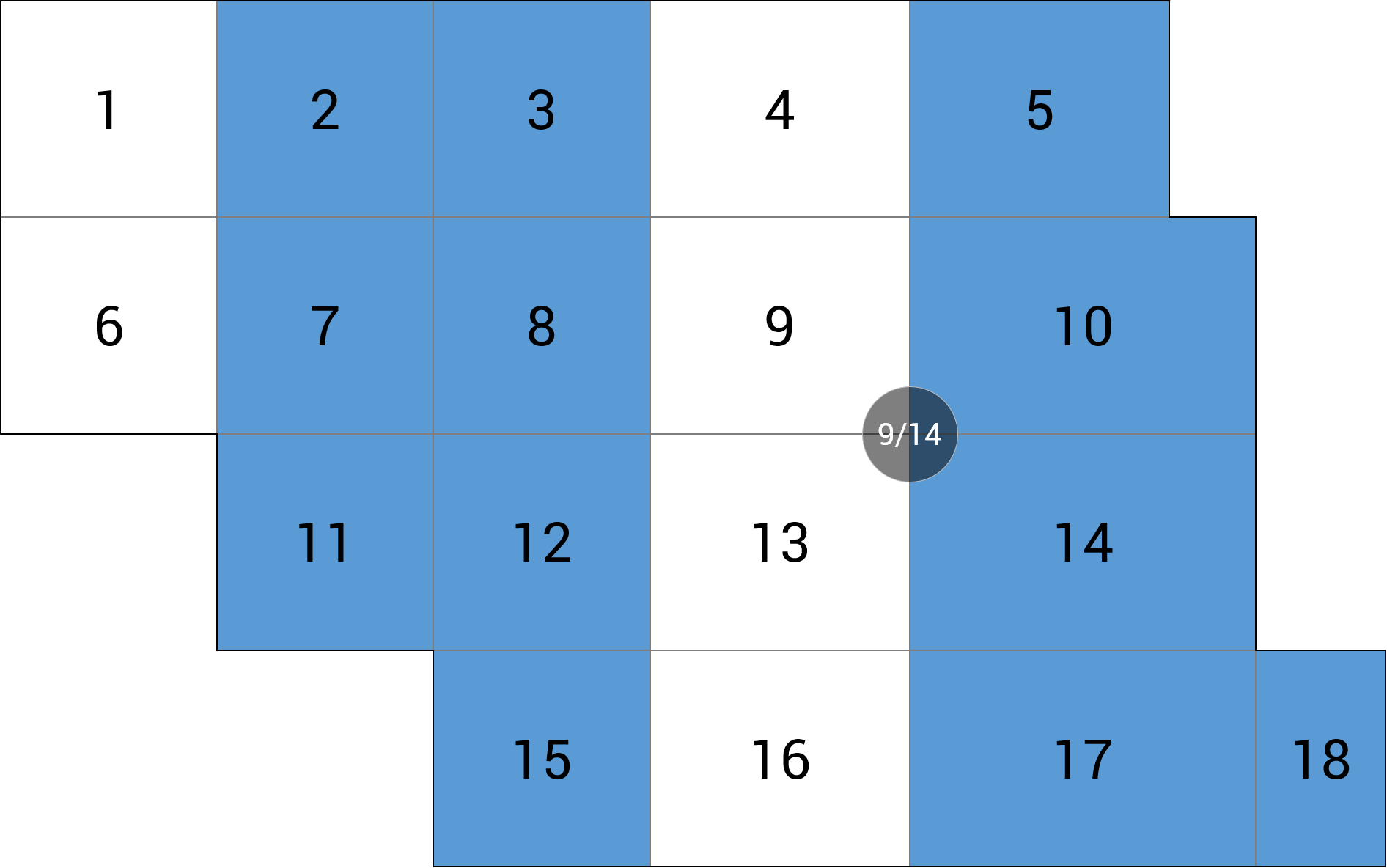 |
MY = -15.27 kNm (-1.4%) |
Tab. 9b Wyniki ugięć dla alternatywnego rozkładu obciążeń zmiennych co 3. pole
| Rozpatrywane miejsce | Schemat obciążenia | Ugięcie [mm] |
|---|---|---|
| a) przęsło wewnętrzne | (Jak dla mx) | -0.89 (-9.2%) |
| b) przęsło skrajne | (Jak dla mx) | -2.37 (-1.7%) |
| c) linia podpór | 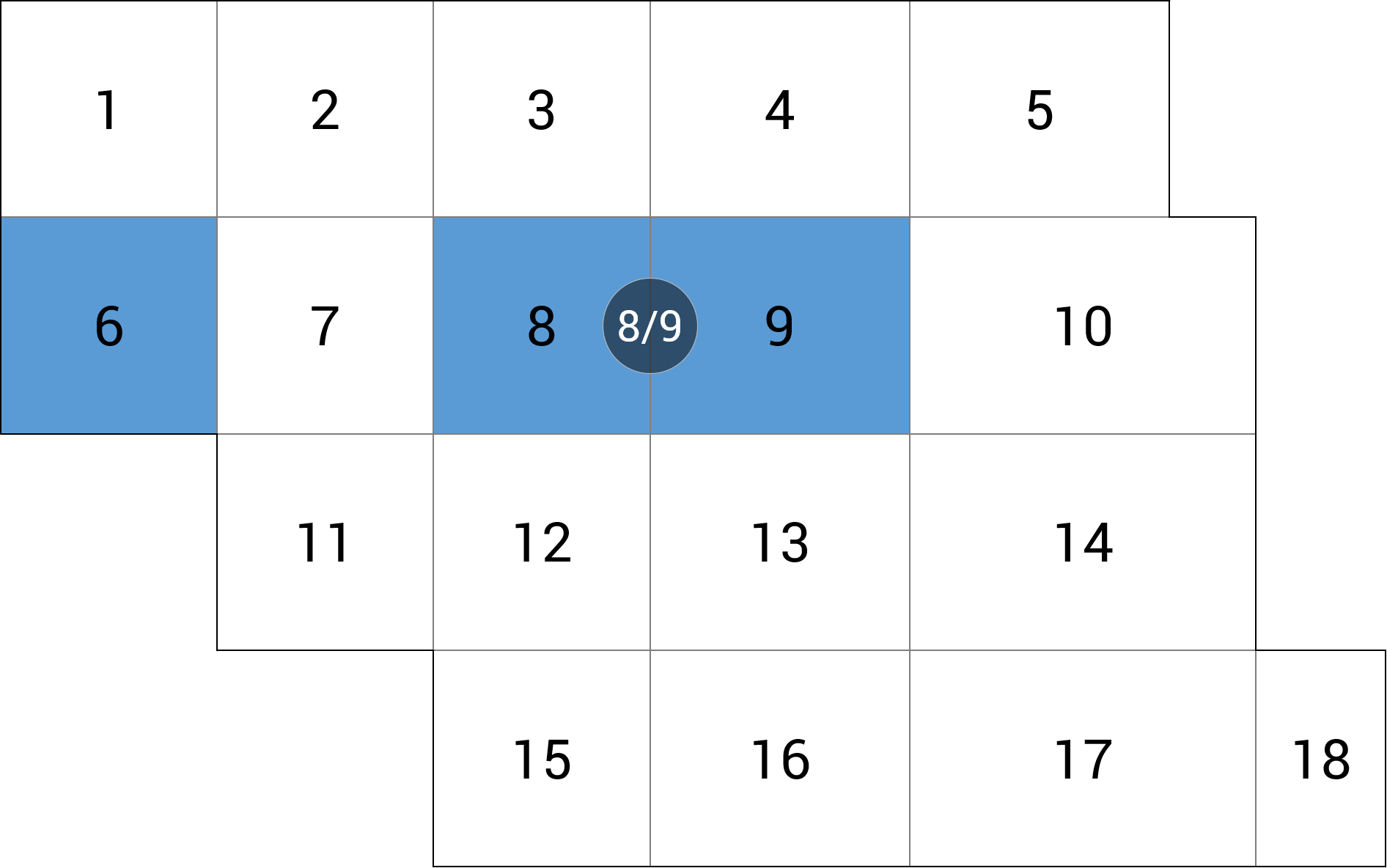 |
-0.43 (-6.5%) |
| d) podpora wewnętrzna | 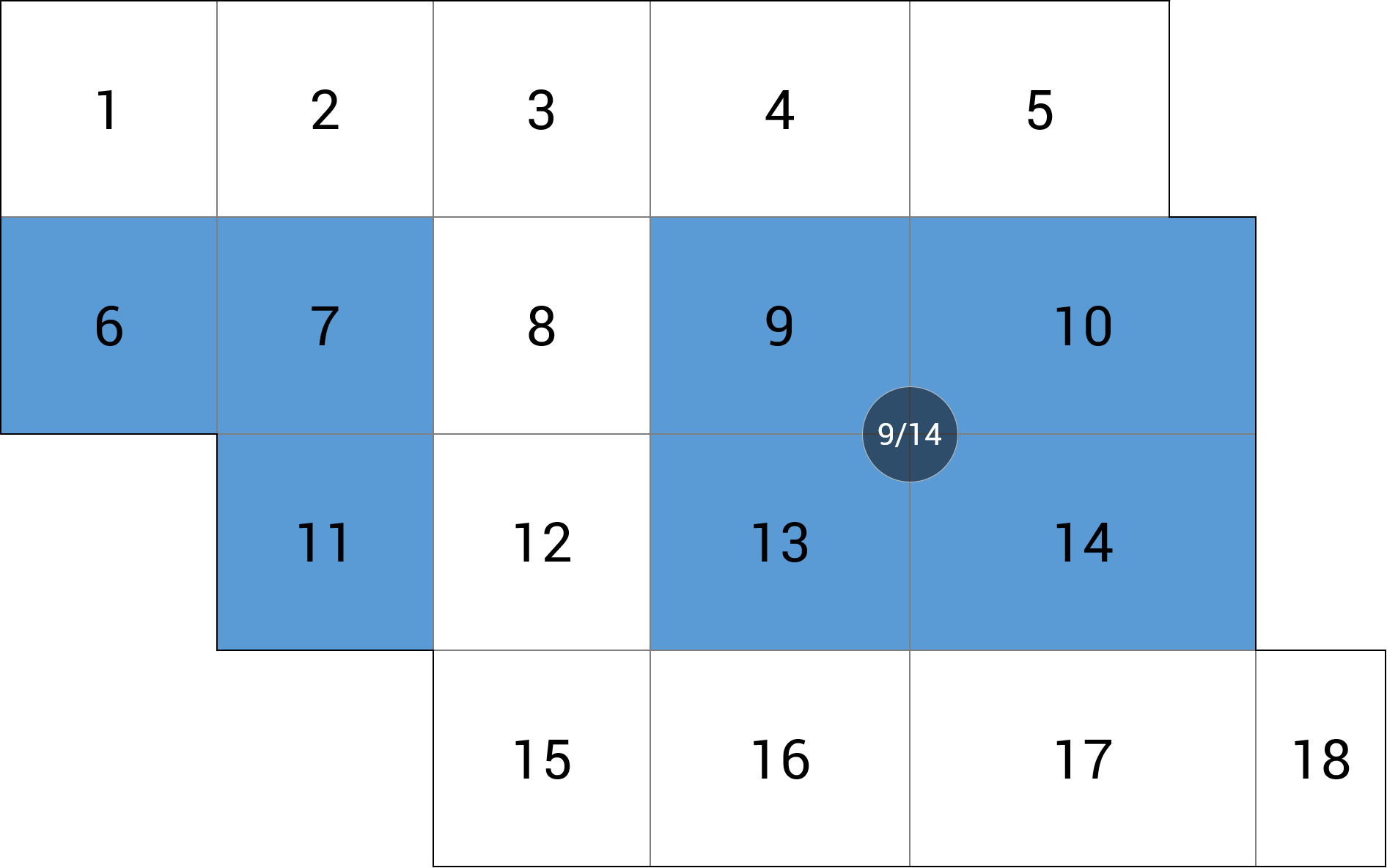 |
RZ = +219.0 kN (-0.6%) |
Zestawienie wyników
Maamy już pogląd na wyniki do poszczególnych sposobów rozkładu obciążeń? Zbierzmy teraz te wyniki razem i rzućmy okiem jakie są różnice pomiędzy nimi. Przyjąłem tutaj założenie, że jeżeli wyniki odbiegają od rozwiązania dokładnego (powierzchni wpływu) o więcej niż 5% (jest to granica umowna i nieostra, ale racjonalna), to dokładność rozwiązania jest wątpliwa. W tablicy 10 zestawiłem wszystkie odchyłki od rozwiązania dokładnego (wartości z pogrubioną czcionką wskazują na pomijalne odchyłki, tj. poniżej 5%).
Tab. 10a Zestawienie odchyłek momentów zginających dla analizowanych schematów rozkładu obciążeń zmiennych (błąd w %)
| Schemat obciążeń | a) przęsło wewnętrzne | b) przęsło skrajne | c) linia podpór | d) podpora (MY) |
|---|---|---|---|---|
| 1. Schemat niezależny | +0.5 | +0.2 | -10.7 | +0.7 |
| 2. Schemat szachownicowy | -37.3 | -33.3 | -47.4 | -61.8 |
| 3. Schemat pasmowy | +0.3 | -0.2 | -11.8 | -62.0 |
| 4a. Schemat na całej pow. x 1.20 | -36.7 | +5.2 | -19.9 | -45.6 |
| 4b. Schemat na całej pow. x 1.30 | -31.4 | +14.0 | -13.2 | -41.1 |
| 5. Schemat rozkładu obciążeń co 2. pole | +0.5 | -0.2 | -28.9 | +0.7 |
| 6. Schemat rozkładu obciążeń co 3. pole | -2.7 | -0.9 | -11.8 | -1.4 |
Tab. 10b Zestawienie odchyłek ugięć dla analizowanych schematów rozkładu obciążeń zmiennych (błąd w %)
| Schemat obciążeń | a) przęsło wewnętrzne | b) przęsło skrajne | c) linia podpór | d) podpora (RZ) |
|---|---|---|---|---|
| 1. Schemat niezależny | -6.1 | -0.4 | +0.0 | -0.5 |
| 2. Schemat szachownicowy | -51.0 | -39.8 | -13.0 | -1.4 |
| 3. Schemat pasmowy | -6.1 | -0.8 | -41.3 | -11.4 |
| 4a. Schemat na całej pow. x 1.20 | -54.1 | -16.2 | -52.2 | +2.2 |
| 4b. Schemat na całej pow. x 1.30 | -54.1 | -16.2 | -52.2 | +10.7 |
| 5. Schemat rozkładu obciążeń co 2. pole | -6.1 | -0.8 | -4.3 | -14.9 |
| 6. Schemat rozkładu obciążeń co 3. pole | -9.2 | -1.7 | -6.5 | -0.6 |
Przeanalizujmy teraz poszczególne schematy. Pierwszy ze schematów – schemat niezależny, daje nam wysoką zgodność wyników dla momentu zginających jak i ugięć względem rozwiązania dokładnego. Błąd wyników oscyluje w założonej granicy 5% – dotyczy to przęsła wewnętrznego i skrajnego jak też linii podpór. Odchyłkę od założonej dokładności dla ugięć w przęśle wewnętrznym (6%) można uznać za pomijalną – kwestia zaokrągleń małych wartości. Jedynie wartość momentu podporowego MY wykazuje błąd bliski 11% (niedoszacowanie), z kolei reakcja podporowa RZ wykazuje błąd bliski 0%.
Co do schematu szachownicowego, to widać wyraźnie, że odchyłki od wartości dokładnych są znaczne. Dla wszystkich analizowanych miejsc błąd względny niedoszacowania momentu zginającego (mx lub MY) wynosi ponad 33%, co jest w każdym wypadku niedopuszczalne. Podobnie jest z błędem ugięć w przęśle wewnętrznym i skrajnym (błąd niedoszacowania powyżej 39%). Mniejszy błąd niedoszacowania daje nam ugięcie w linii podpór (13%), mimo wszystko jest on większy niż przyjęta tolerancja 5%. Jedynie wartość reakcji podporowej RZ (ok. 1%) jest zbliżona do wartości dokładnej otrzymanej z powierzchni wpływu.
Wyniki dla schematu pasmowego można podzielić na dwie grupy. Pierwsza z nich dotyczy wartości w przęsłach (momenty dodatnie – rozciąganie dołem), druga – obszarów, gdzie występują momenty ujemne (rozciąganie górą). Wyniki obliczeń w grupie pierwszej, czyli momenty i ugięcia w przęśle wewnętrznym i skrajnym, dają nam błąd oscylujący w granicy 5% (błąd ugięć 6% w przęśle wewnętrznym, podobnie jak w schemacie niezależnym, można uznać za akceptowalny).
Druga grupa wyników schematu pasmowego – obszary momentów ujemnych – wykazują już znaczące odchyłki. Błąd względny dla momentu mX w linii podpór wynosi ok. 12% (niedoszacowanie), z kolei ugięcie w tym miejscu wykazuje błąd niedoszacowania ponad 41%. Jeśli chodzi o wartość momentu podporowego MY, to błąd niedoszacowania jest jeszcze większy i wynosi 62%. Niedoszacowanie reakcji podporowej RZ na tej podporze wynosi ok. 11%.
Oba schematy obciążenia ze współczynnikiem zwiększającym (faktor 1.20 oraz 1.30) wykazują znaczące odchylenia. I tak błąd względny momentów mX i ugięć w przęśle wewnętrznym wynoszą odpowiednio ponad 31% oraz 54% (oba błędy niedoszacowania). Odchyłka momentu mX w przęśle skrajnym wynosi dla faktora = 1.20: ok. 5% (nadmiar) a dla 1.30: 14% (nadmiar). Inaczej mają się ugięcia w tym miejscu – dla obu schematów błąd niedoszacowania wynosi ok. 16%.
Wartości w linii podpór w obu schematach wykazują znaczące odchylenia od założonej dokładności. Niedoszacowanie momentu mX w linii podpór wynosi ok. 20% oraz 13% odpowiednio dla współczynnika 1.20 oraz 1.30. Natomiast błąd ugięć przekracza 52% (niedoszacowanie).
Wartość momentu podporowego MY w obu schematach przekracza 41% niedoszacowania, reakcja podporowa wykazuje mniejszy błąd zawyżenia na poziomie 2% (faktor 1.20) oraz 11% (faktor 1.30).
Schemat rozkładu obciążenia co 2. pole wykazuje w strefach przęsłowych błąd w granicy 5% zarówno dla momentu mX jak i ugięcia. Błąd ugięcia przęsła wewnętrznego na poziomie 6% uznałem za akceptowalny (por. schemat niezależny).
Moment mX w linii podpór odbiega już jednak znacząco od rozwiązania dokładnego (ok. 29% niedoszacowania). Inaczej jest z ugięciem w tym miejscu, gdzie błąd niedoszacowania jest poniżej 5%.
Wartość momentu podporowego MY jest bliska wyniku dokładnego (1%), w przeciwieństwie do wartości reakcji podporowej RZ, gdzie błąd niedoszacowania wynosi blisko 15%.
Schemat rozkładu obciążenia co 3. pole, w odniesieniu do stref przęsłowych, daje mniej więcej podobne wyniki jak rozkład co 2. pole. Moment mX i ugięcia nie odbiegają od wyniku dokładnego o więcej niż 3%. Wyjątkiem jest wartość ugięcia w przęśle wewnętrznym, gdzie błąd niedoszacowania wynosi 9%.
Moment zginający mX w linii podpór zawiera błąd niedoszacowania na poziomie 12%, z kolei błąd ugięcia w tym obszarze wynosi ok. 7%. Obie wartości przekraczają założoną dokładność 5%. Ten ostatni błąd (tj. 7%) można jednak uznać kompromisowo – konsekwentnie jak w schemacie niezależnym – za akceptowalny.
Znacznie lepiej jest z wartościami podporowymi – zarówno błąd względny momentu MY jak i reakcji RZ wykazują błąd bliski rozwiązaniu dokładnemu (poniżej 2%).
Wnioski
Podsumowując wszystkie 6 analizowane schematy rozkładu obciążenia zmiennego dla stropu płytowo-belkowego możemy określić, które ze schematów nadają się w tego typu konstrukcji. Kolejność schematów podałem od największej do najmniejszej dokładności.
- Mamy dwa schematy rozkładu obciążeń zmiennych o względnie wysokiej dokładności wyników. Najdokładniejszym z nich jest schemat obciążeń niezależnych, w którym błąd względny analizowanych miejsc oscyluje na poziomie 5%. Jedynym wyjątkiem jest wartość momenty mX w linii podpór (błąd niedoszacowania 11%).
- Drugim, równie dokładnym schematem jest schemat rozkładu obciążenia co 3. pole. Podobnie jak w schemacie niezależnym większość odchyłek mieści się w granicach błędu 5%. Również wartość momentu mX w linii podpór wykazuje błąd niedoszacowania zbliżony do pierwszego schematu (12%). Jedyną znaczącą różnicą w zestawieniu ze schematem niezależnym jest to, że ugięcie w przęśle wewnętrznym w schemacie co 3. pole wykazuje błąd niedoszacowania równy 9% (większy niż założone 5%). Mówiąc krótko, w tym schemacie trzeba mieć świadomość, że ugięcia i momenty ujemne mogą być nieznacznie zaniżone.
- Schemat obciążeń co 2. pole daje poprawne wyniki większości momentów zginających jak też ugięć. Wyjątek stanowi moment mX w linii podpór (nad belką), gdzie błąd zaniżenia wynosi 29%. Wartość reakcji podporowej RZ jest zaniżona o ok. 15%.
- Schemat pasmowy, podobnie do schematu co 2. pole, daje miarodajne wyniki momentów zginających i ugięć w obszarze momentów przęsłowych (błąd 5%). Natomiast w obszarze momentów ujemnych (rozciąganie górą) wartości wyników w tym schemacie przekraczają dopuszczalne odchylenia od rozwiązania dokładnego z powierzchni wpływu (rozrzut błędu niedoszacowania 12 do 62%).
- Schemat obciążenia ze współczynnikiem zwiększającym 1.20 oraz 1.30. W zasadzie oprócz wartości momentów mX w linii podpór (zapas błędu od 5 do 14%) oraz reakcji podporowej RZ (zapas błędu 2 do 10%), wartości nie dają zadowalającej zgodności z rozwiązaniem otrzymanym z powierzchni wpływu (błąd niedoszacowania w graniach 13 do 54%).
- Schemat szachownicowy w odniesieniu do stropów płytowo-belkowych jest metodą nieakceptowalną. Błędy wynikające z zastosowania tego podejścia w tego typu stropach wynoszą dla momentów zginających ponad 33% a dla ugięć co najmniej 13%.
Jak widzisz, najbardziej kompromisowymi rozwiązaniami pod kątem nakładu pracy i dokładności wyników rozkładu obciążenia zmiennego na stropie płytowo-belkowym jest schemat niezależny oraz obciążenie co 3. pole. Mimo ich niedoskonałości spełniają zasadniczo swój cel. Pamiętać jedynie należy, że wyniki ugięć oraz momentów dodatnich mogą być nieznacznie zaniżone.
Na pewno zauważyłeś, że nie wszystkie tak chętnie stosowane na co dzień schematy rozkładu obciążeń zmiennych (np. szachownica) sprawdzają się w stropach płytowo-słupowych? Przyjęcie sposobu rozkładu obciążeń wymaga zawsze ostrożności i zastanowienia.
Moim zdaniem wyłaniają się tutaj dwie sensowne w użyciu metody rozkładu obciążeń: (1) schemat obciążeń niezależnych i (2) schemat rozkładu obciążenia co 3. pole.
Co o tym myślisz? Jeśli masz pytania, pisz śmiało w komentarzach. Chętnie poznam Twoje spojrzenie na ten temat.
Powodzenia!

Wpisy z cyklu „Rozkład obciążeń zmiennych„:
- Powierzchnie wpływu,
- Strop płytowo-słupowy,
- Strop płytowo-słupowy – metody alternatywne,
- Strop płytowo-belkowy,
- Strop oparty na ścianach (w opracowaniu).
Źródła
- Starosolski W., Aneks do: Wybrane zagadnienia komputerowego modelowania konstrukcji inżynierskich, na prawach rękopisu, Pro-Soft, Gliwice 2007,
- Starosolski W., Komputerowe modelowanie betonowych ustrojów inżynierskich. Wybrane zagadnienia, t.1 i 2, Wyd. Politechniki Śląskiej, Gliwice 2009,
- Starosolski W., Wybrane zagadnienia komputerowego modelowania konstrukcji inżynierskich, Wyd. Politechniki Śląskiej, Gliwice 2003,
- Zdanowicz Ł., Praca magisterska: Analiza obliczeniowa i projekt konstrukcji wielokondygnacyjnego budynku o ustroju płytowo-słupowym, Kraków 2010.



O rozkładzie obciążeń „w szachownicę” uczyli mnie jeszcze na studiach. Czas chyba zweryfikować wiadomości. Błąd niedoszacowania aż 30%, jak to możliwe?
Racja, racja, 30% to dużo! Podejrzewam że na studiach uczą często mieszając metody stare z nowymi. I tak np. metoda szachownicowa była używana kiedy każdy element konstrukcji obliczano osobno (strop, belki, słupy itd.). Tutaj wykorzystywało się tablice Winklera, które tam się sprawdzały (nakład pracy) i stworzone były właśnie na bazie szachownicy w jednym kierunku.
Takich tematów jest więcej – trzeba być czujnym ;)
Czekam zatem na kolejne ciekawe artykuły :)