Dzisiaj rozwijam dalej temat rozkładu obciążeń zmiennych na stropach. Pytanie przewodnie brzmi: jak prawidłowo rozkładać obciążenia zmienne na stropie płytowo-słupowym? Przedstawię wam zasadnicze różnice pomiędzy pięcioma najpowszechniejszymi sposobami rozkładu obciążeń na konkretnym przykładzie. Zestawię i porównam dokładność wyników dla każdego ze sposobów i na koniec podam wnioski do wykorzystania w projektowaniu stropów typu płyta-słup.
W poprzednim wpisie dotyczącym powierzchni wpływu określiłem cel, jaki chcemy osiągnąć. Pamiętacie? Chodzi o uzyskanie możliwie najbardziej niekorzystnego schematu rozkładu obciążeń zmiennych, wywołującego ekstremalne ugięcia i siły wewnętrzne.
Jak się domyślacie najdokładniejszą metodą rozkładu obciążeń zmiennych jest rozłożenie obciążenia wg przebiegu powierzchni wpływu. Jest to jednak praktycznie niemożliwe z uwagi na ilość pracy, jaką trzeba by przy tym wykonać (tysiące przypadków obciążeń!). Jaki więc sposób rozkładu obciążenia zmiennego dla stropów płytowo-słupowych jest najefektywniejszy? Jak skutecznie ograniczyć liczbę schematów obciążeń zmiennych? Który ze sposób wymaga najmniej nakładu pracy (ekonomia) i jednocześnie gwarantuje miarodajne wyniki (bezpieczeństwo)? Dalej, sprawdźmy to!
Model obliczeniowy stropu płytowo-słupowego
Do analizy rozkładu obciążeń na stropie płytowo-słupowym wykorzystam przykład, który analizowałem we wpisie omawiającym powierzchnie wpływu.
Powtórzę tutaj podstawowe dane: strop o 18-tu polach (rys. 1), rozpiętości przęseł od 3.0 m do 8.0 m, grubość płyty h = 0.20 m, wysokość kondygnacji H = 3.0 m, słupy kwadratowe o wymiarach boków b = 0.30 m. Podział płyty na elementy skończone (ES) pokazano na rys. 2. Materiał: beton C30/37. Założone obciążenie zmienne q = 5.0 kN/m2.

Rys. 1 Geometria stropu i podział pól obciążenia

Rys. 2 Model obliczeniowy stropu (3240 ES)
Powierzchnie wpływu
W poprzednim wpisie pokazałem wam w jaki sposób wyznaczyć powierzchnie wpływu dla wybranych wielkości. Pozwalają one określić, które obszary stropu należy obciążyć, żeby uzyskać maksymalne wartości ugięcia, momentu zginającego czy innych analizowanych wielkości. Metoda jest w miarę prosta w zastosowaniu i daje konkretną odpowiedź, które z obszarów należy obciążyć.
W tabeli 1 zebrałem obrazy powierzchni wpływu stropu płytowo-słupowego dla momentów zginających i ugięć dla 4 charakterystycznych miejsc stropu: a) przęsło wewnętrzne, b) przęsło skrajne, c) w linii podpór oraz d) podpora. Szczegóły i wyniki zostały omówione w przywołanym wcześniej wpisie dot. powierzchni wpływu. Tutaj nie będę tego powtarzać.
Tab. 1 Przebieg granic powierzchni wpływu dla wybranych miejsc
| Miejsce | Dla momentu zginającego | Dla ugięcia |
|---|---|---|
| a) przęsło wewnętrzne | 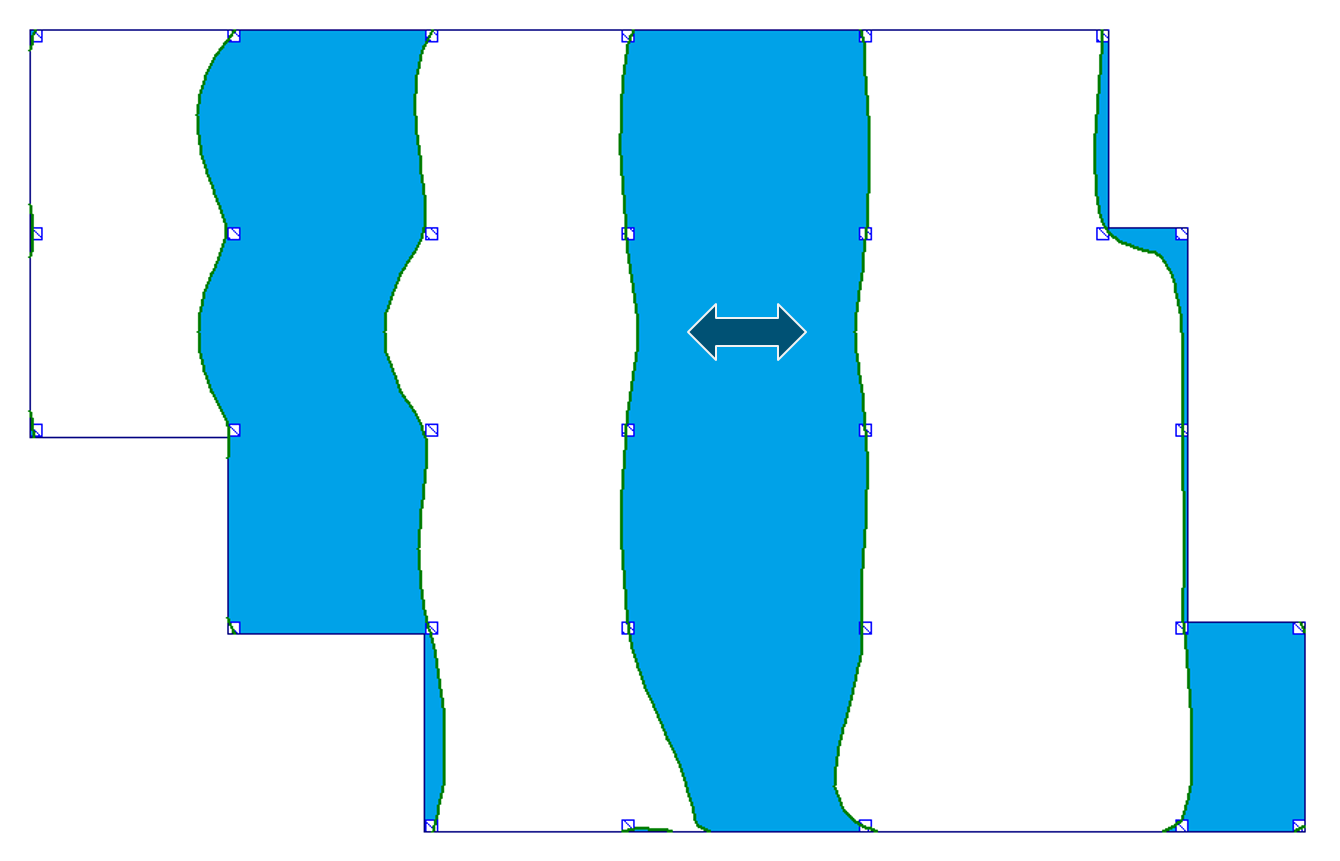 |
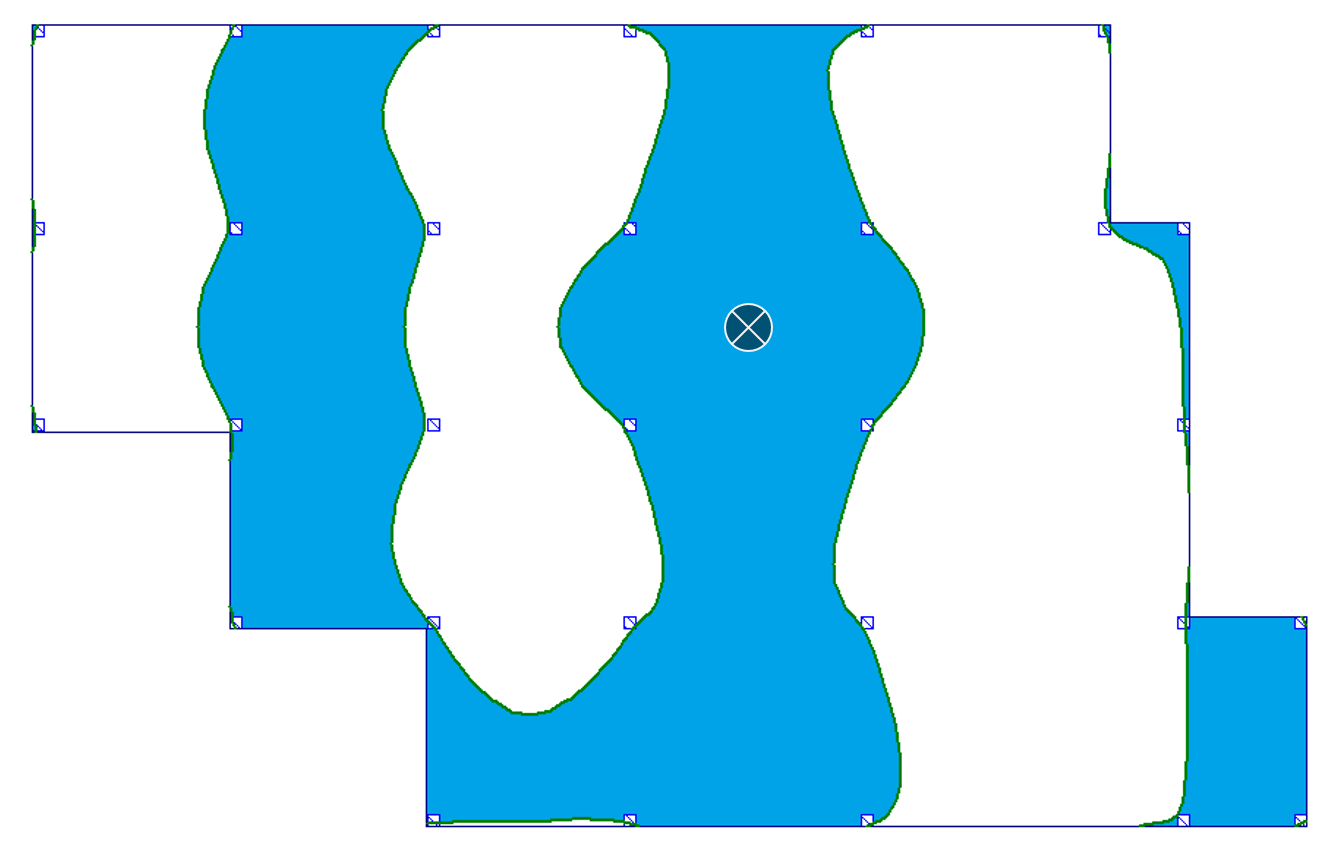 |
| b) przęsło skrajne | 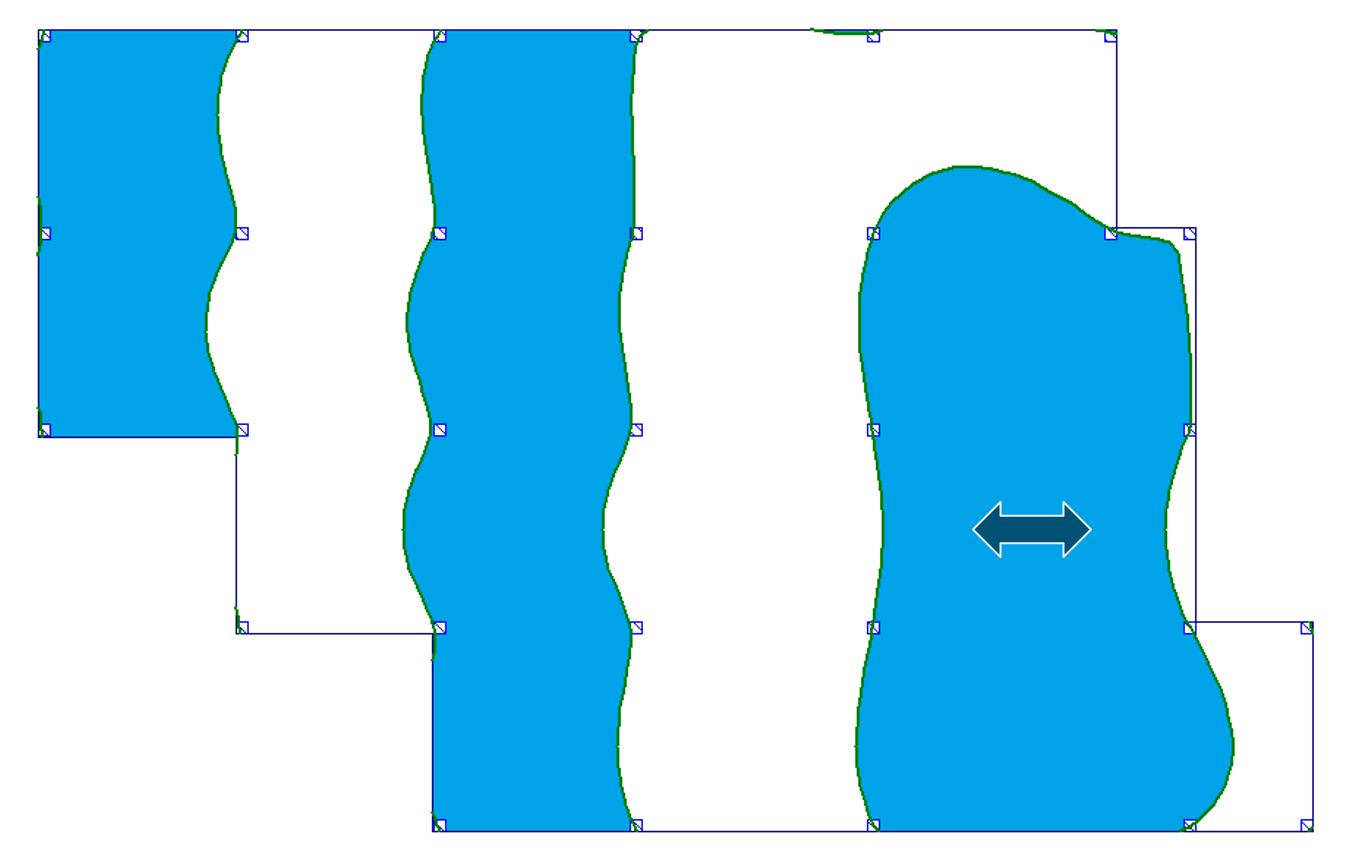 |
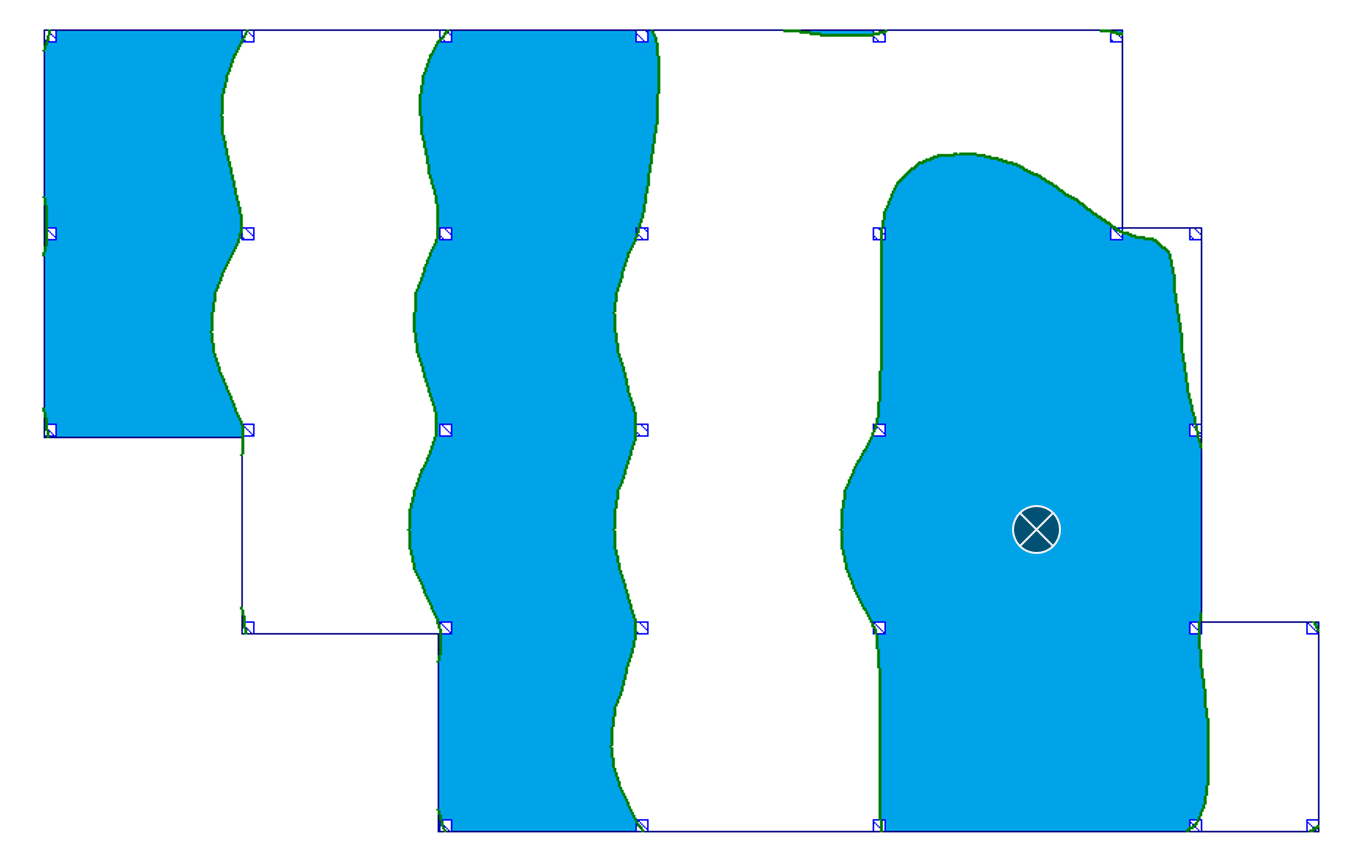 |
| c) w linii podpór | 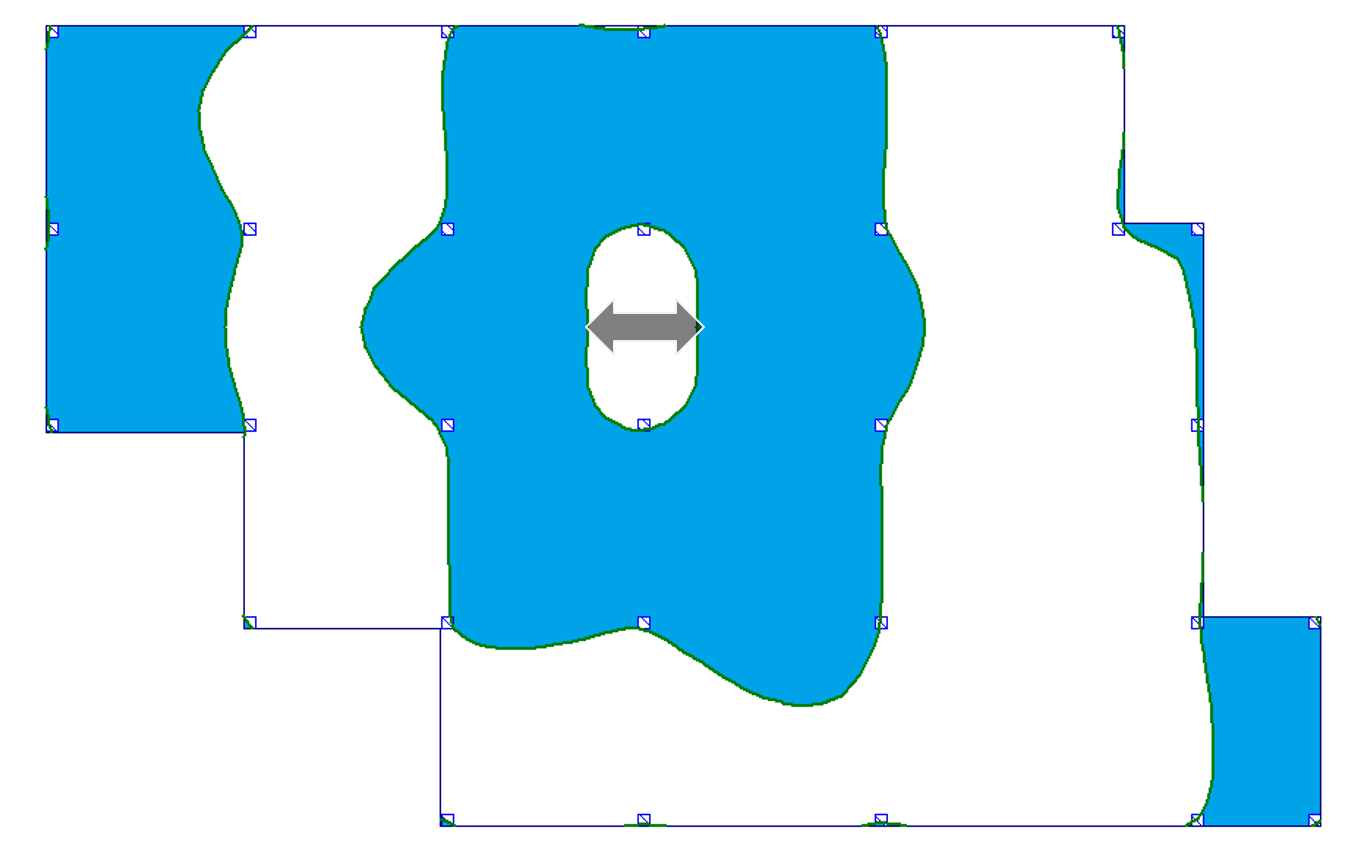 |
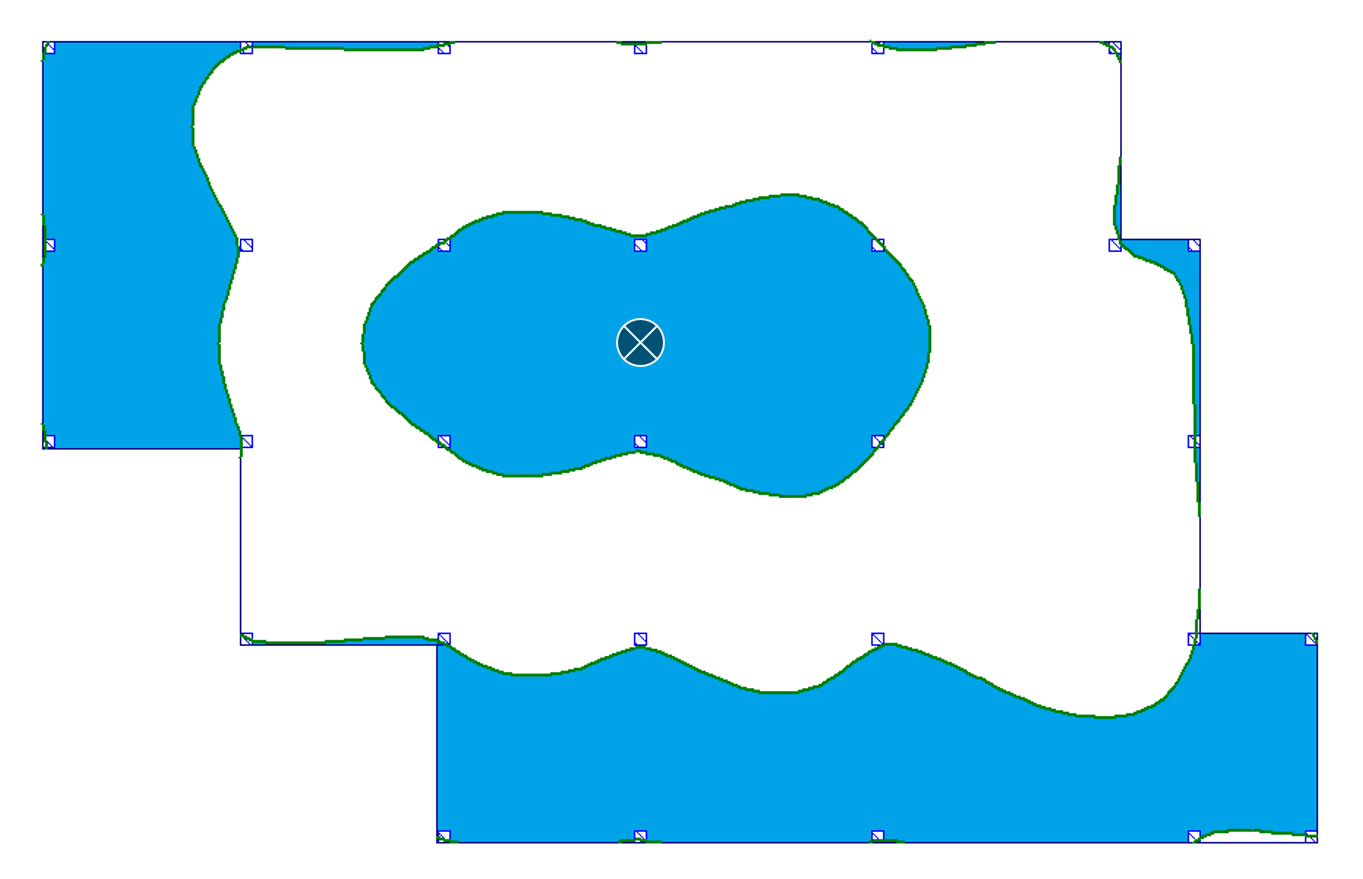 |
| d) podpora wewnętrzna (moment i reakcja podporowa) | 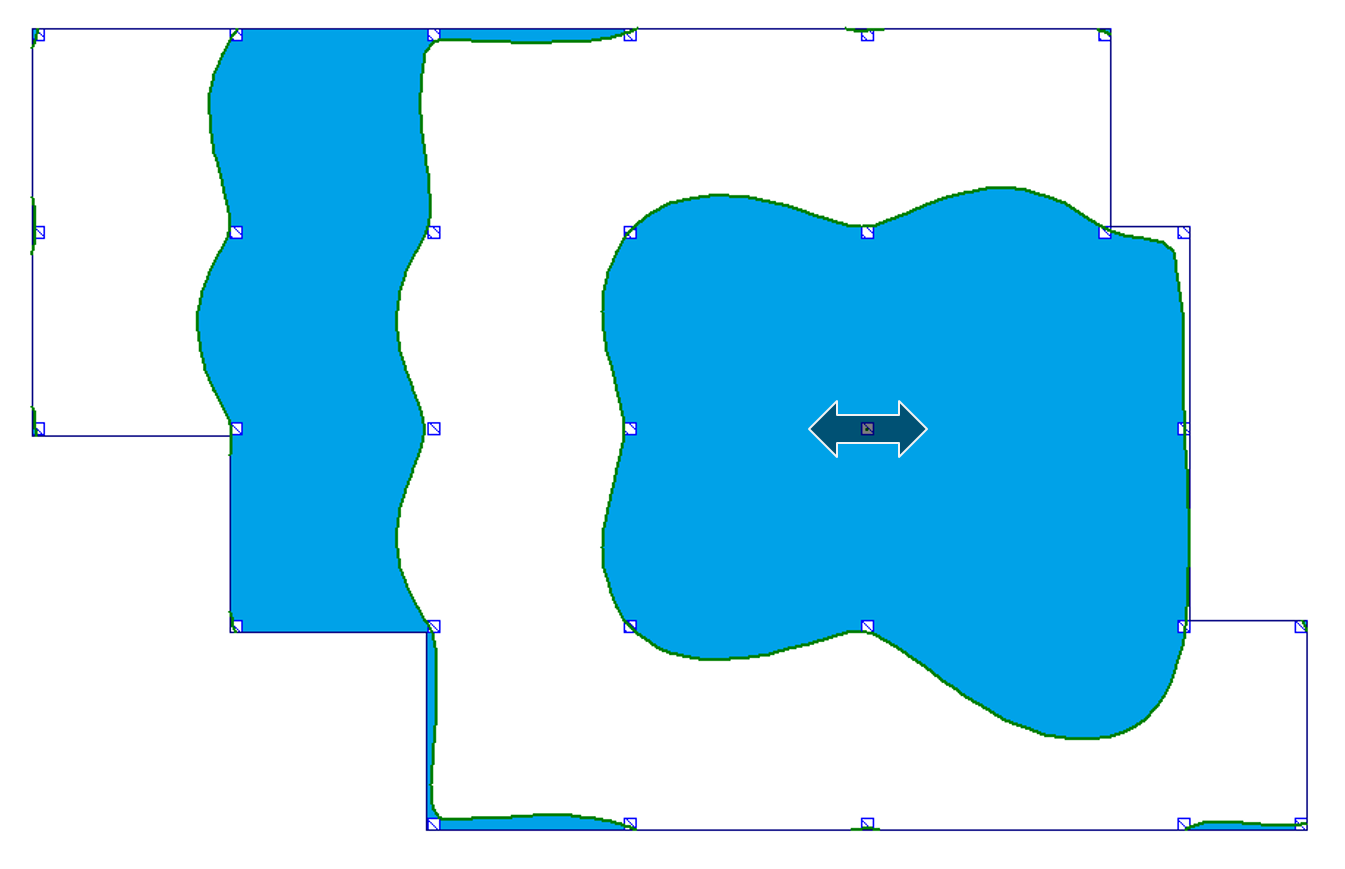 |
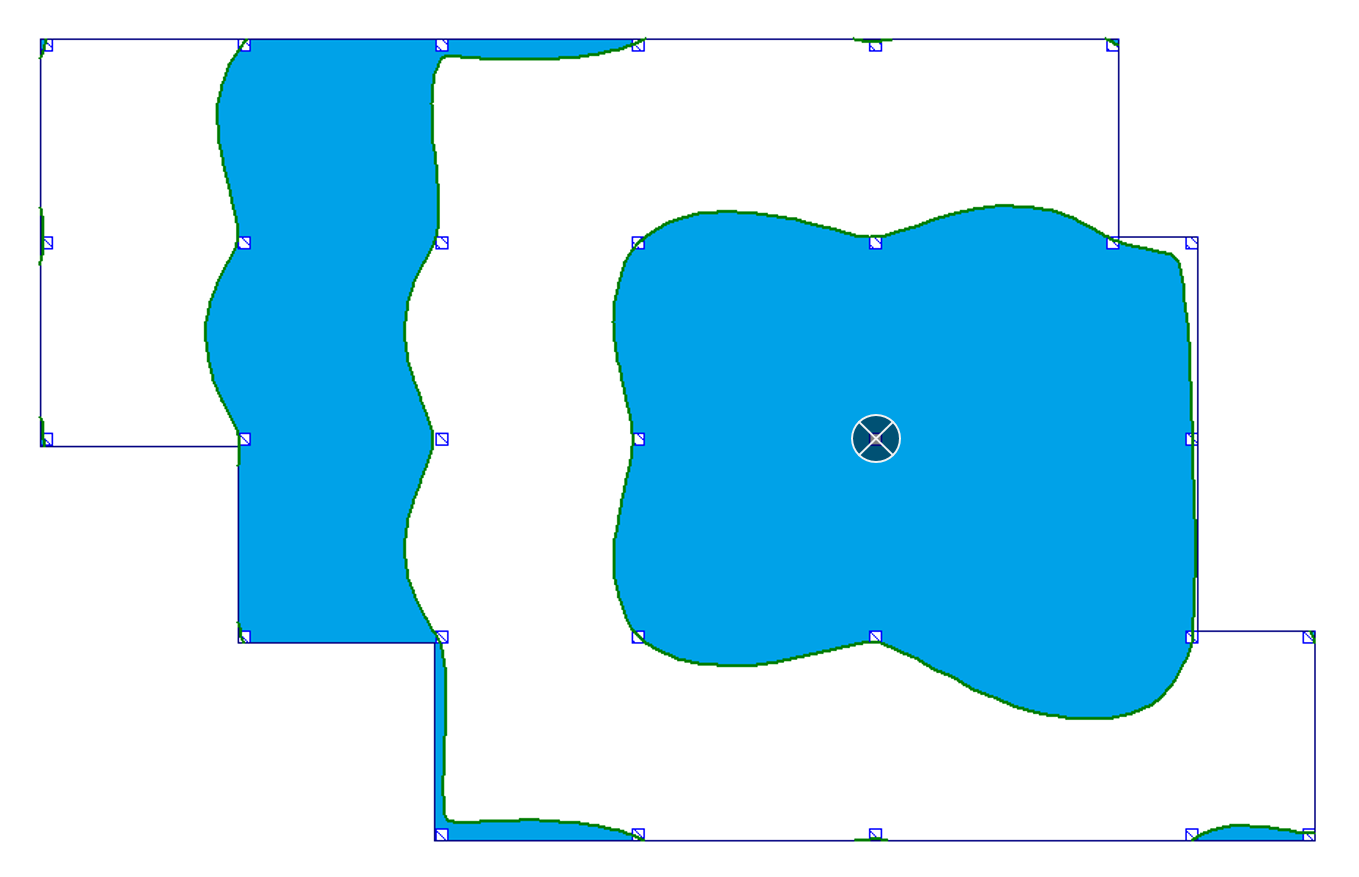 |
Metody rozkładu obciążeń zmiennych
Skoro wiemy już jak wyglądają powierzchnie wpływu dla wybranych wielkości, wróćmy teraz do tematu rozkładu obciążeń zmiennych na stropach w praktyce projektowej. Najczęściej spotykanymi w codziennej praktyce schematami rozkładu obciążeń zmiennych są:
- schemat obciążeń niezależnych – polega na przyłożeniu pojedynczych obciążeń na każde pole płyty w ramach jednego przypadku obciążeń. Wartości ekstremalne otrzymuje się za pomocą kombinacji tych przypadków. Liczba przypadków obciążeń równa jest liczbie wydzielonych pól.
- schemat szachownicowy – tradycyjny sposób rozkładu obciążeń zmiennych polegający na rozkładzie obciążeń na wzór planszy szachownicowej, tj. każde obciążone pole płyty rozdzielone jest w kierunkach ortogonalnych polem nieobciążonym. Wyjątek stanowi obciążenie stref podporowych stropu, gdzie odpowiednie obciążone pola płyty sąsiadują ze sobą.
- schemat pasmowy – sposób rozkładu obciążeń zaczerpnięty z metody ram zastępczych, gdzie dla otrzymania poszczególnych ekstremalnych wartości sił i ugięć płytę stropu obciąża się pasmowo w jednym kierunku,
- obciążenie na całej powierzchni stropu ze współczynnikiem zwiększającym – taki sposób rozkładu obciążeń spotkałem w mojej praktyce raz czy dwa. Polega na rozłożeniu obciążeń zmiennych na całej powierzchni stropu w ramach jednego przypadku obciążenia (analogia do obciążeń stałych), którego wartość została zwiększona przez zastosowanie współczynnika zwiększającego (faktor = 1.20 do 1.30). Idea polegać ma na tym, żeby jak najprościej rozłożyć obciążenie zmienne na stropie w ramach jednego przypadku obciążenia zmiennego na całym stropie.
Na pierwszy rzut oka najbardziej skutecznym rozwiązaniem wydaje się być schemat rozkładu obciążeń niezależnych. Ale co w przypadku jeśli mamy do zaprojektowania rozległy strop np. o 36 polach obciążeń albo i więcej? Czy taki nakład pracy i tworzenie dziesiątek czy setek przypadków obciążeń będzie miało sens? Czy z kolei schemat szachownicowy, mimo swojej prostoty, jest odpowiedni i czy daje nam pewność, że wyniki obliczeń są poprawne? Czy uwzględnia wszystkie niekorzystne sytuacje? Albo czy schemat pasmowy jest wystarczający i możemy być pewni, że projektujemy bezpiecznie? A może obciążenie na całej powierzchni stropu zwiększone o odpowiedni faktor? Ale czy to nie jest zbyt wielkie uproszczenie? Czy aby, oprócz zwiększonej globalnie sumy obciążeń, nie powoduje on wyników znaczenie odbiegających od rzeczywistych wielkości, w tym błędów niedomiaru?
Co do tego, który ze schematów rozkładu obciążeń zmiennych jest najskuteczniejszy i jednocześnie najrozsądniejszy, pewności nie mamy. Dlatego sprawdzimy to.
Porównanie wyników metod rozkładu obciążeń zmiennych
Przedstawię wam wyniki dla opisanych wyżej schematów w zestawieniu z rozwiązaniem dokładnym, czyli uzyskanego z powierzchni wpływu. Przyjmijmy tutaj, że akceptowalny błąd obliczeń względem rozwiązania dokładnego jest na poziomie ok. 5%. Na tej podstawie będzie można ocenić, który ze sposobów jest najwłaściwszy – zarówno pod kątem wiarygodności wyników jak i nakładu pracy.
W tej analizie przebadałem 5 sposobów rozkładu obciążeń zmiennych:
- Schemat obciążeń niezależnych,
- Schemat szachownicowy,
- Schemat pasmowy,
- Obciążenie na całej powierzchni x Faktor = 1.20,
- Obciążenie na całej powierzchni x Faktor = 1.30,
Poniższe tabele prezentują wyniki obliczeń i ich różnice dla każdego ze schematów. Wartości procentowe (%) prezentują różnice błędu w odniesieniu do rozwiązania dokładnego, gdzie znak „-” (minus) oznacza niedomiar.
0. Rozkład obciążeń wg przebiegu powierzchni wpływu
Uwaga techniczna: Jeśli chodzi o wyniki uzyskane z powierzchni wpływu, to otrzymano je zakładając obciążenie na powierzchni mniejszej lub równej 1 m2 płyty jako osobny przypadek obciążenia. Dało to 563 przypadków obciążenia. Jest to oczywiście pewien kompromis. Gdyby zakładać obciążenia osobno na każdym elemencie skończonym (przeciętny wymiar elementu skończonego to 0.5 m x 0.5 m), to liczba przypadków obciążeń wzrosłaby do 3240, co prowadzi do granic możliwości obliczeniowych programu MES… i moich też ;)
Tab. 2a Wyniki momentów zginających dla rozkładu obciążeń wg powierzchni wpływu
| Rozpatrywane miejsce | Schemat obciążenia | Moment mX [kNm/m] |
|---|---|---|
| a) przęsło wewnętrzne | (Por. pow. wpływu – tab.1) | +12.41 (—) |
| b) przęsło skrajne | (Por. pow. wpływu – tab.1) | +21.80 (—) |
| c) linia podpór | (Por. pow. wpływu – tab.1) | -8.33 (—) |
| d) podpora wewnętrzna | (Por. pow. wpływu – tab.1) | MY = -25.64 kNm (—) |
Tab. 2b Wyniki ugięć dla rozkładu obciążeń wg powierzchni wpływu
| Rozpatrywane miejsce | Schemat obciążenia | Ugięcie [mm] |
|---|---|---|
| a) przęsło wewnętrzne | (Por. pow. wpływu – tab.1) | -2.21 (—) |
| b) przęsło skrajne | (Por. pow. wpływu – tab.1) | -5.85 (—) |
| c) linia podpór | (Por. pow. wpływu – tab.1) | -1.22 (—) |
| d) podpora wewnętrzna | (Por. pow. wpływu – tab.1) | RZ = +209.1 kN (—) |
1. Schemat obciążeń niezależnych
Tab. 3a Schemat obciążeń i wyniki momentów zginających dla niezależnego rozkładu obciążeń
| Rozpatrywane miejsce | Schemat obciążenia | Moment mx [kNm/m] |
|---|---|---|
| a) przęsło wewnętrzne | 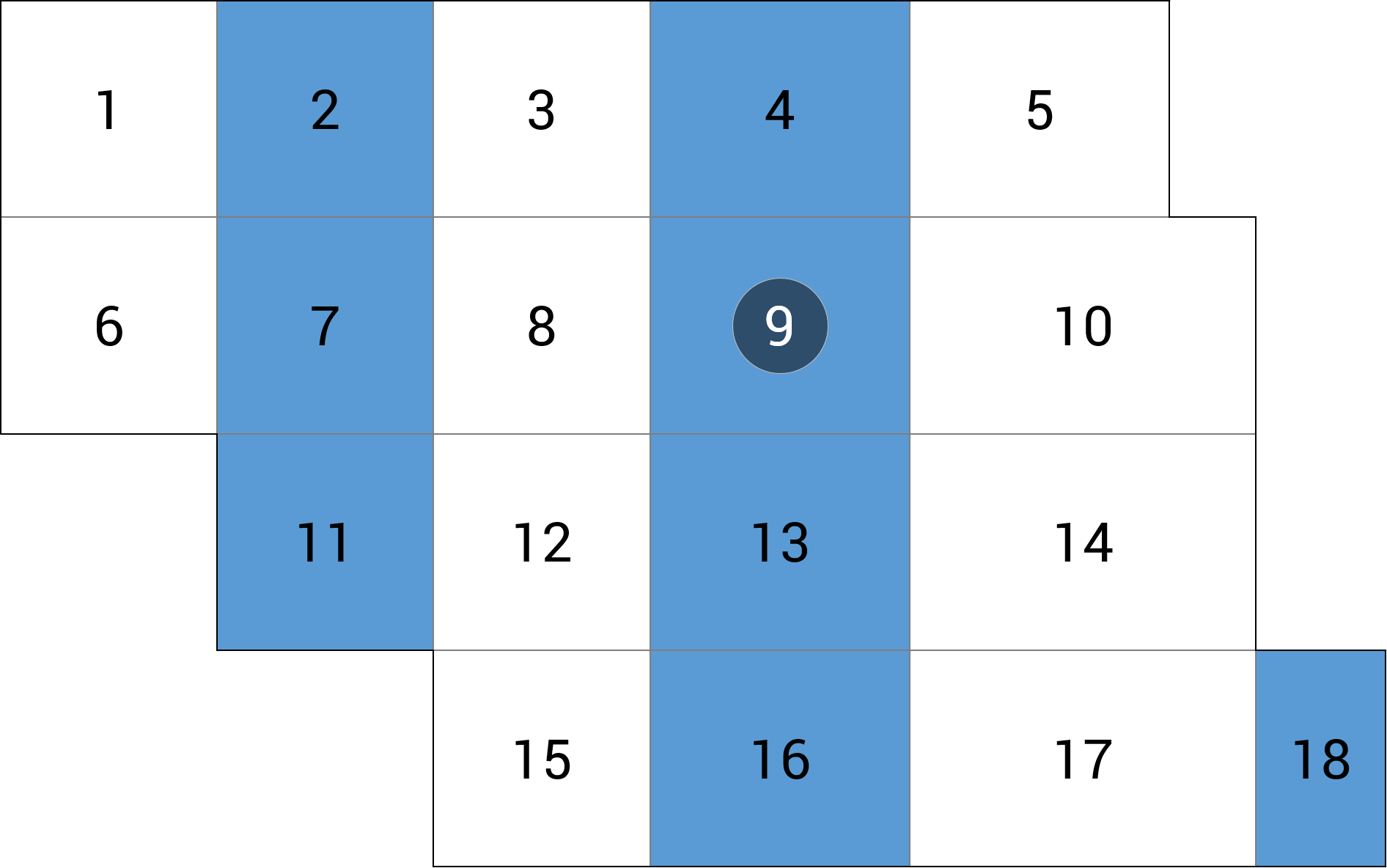 |
+12.53 (0.8%) |
| b) przęsło skrajne |  |
+21.66 (-0.6%) |
| c) linia podpór | 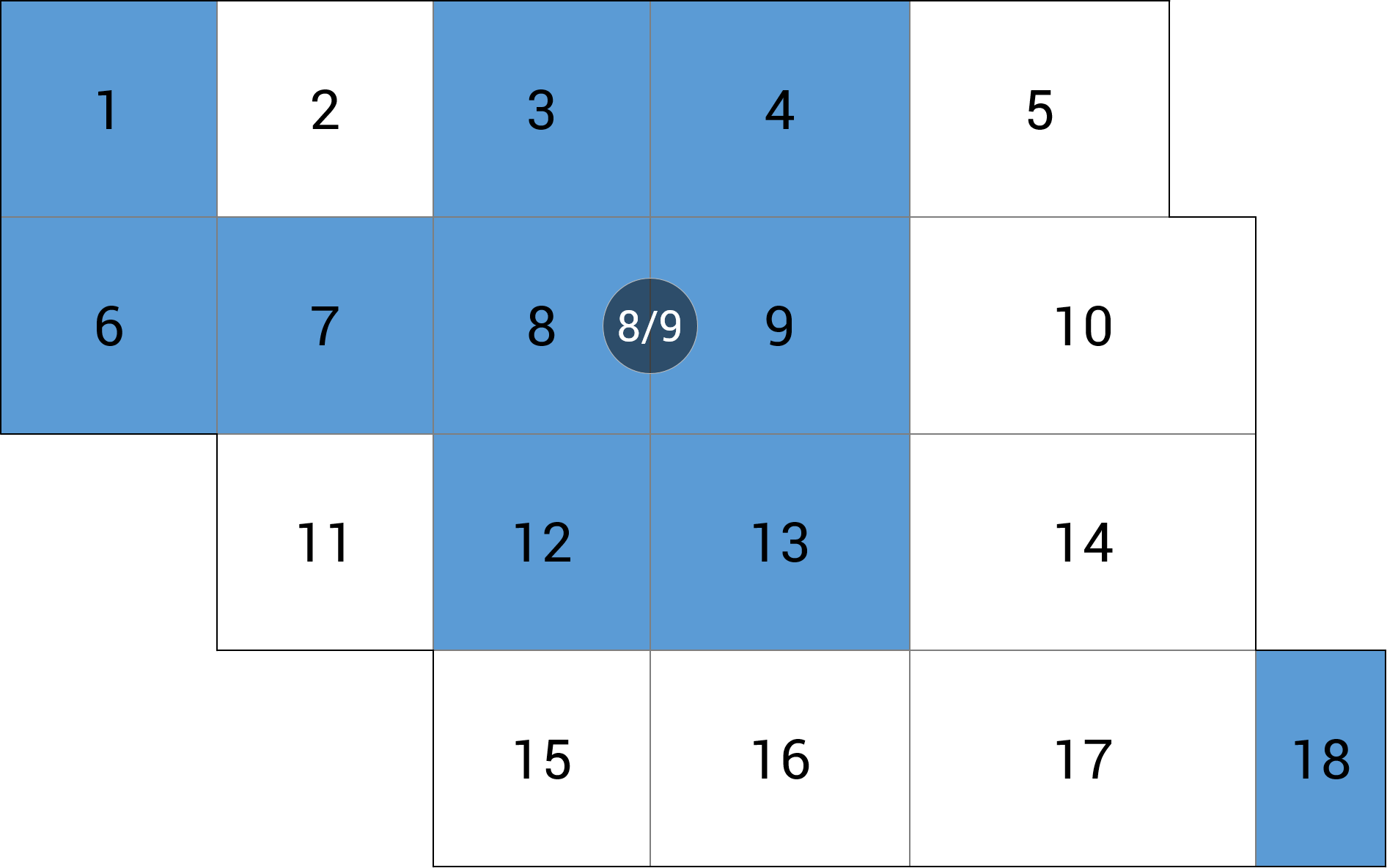 |
-5.69 (-31.7%) |
| d) podpora | 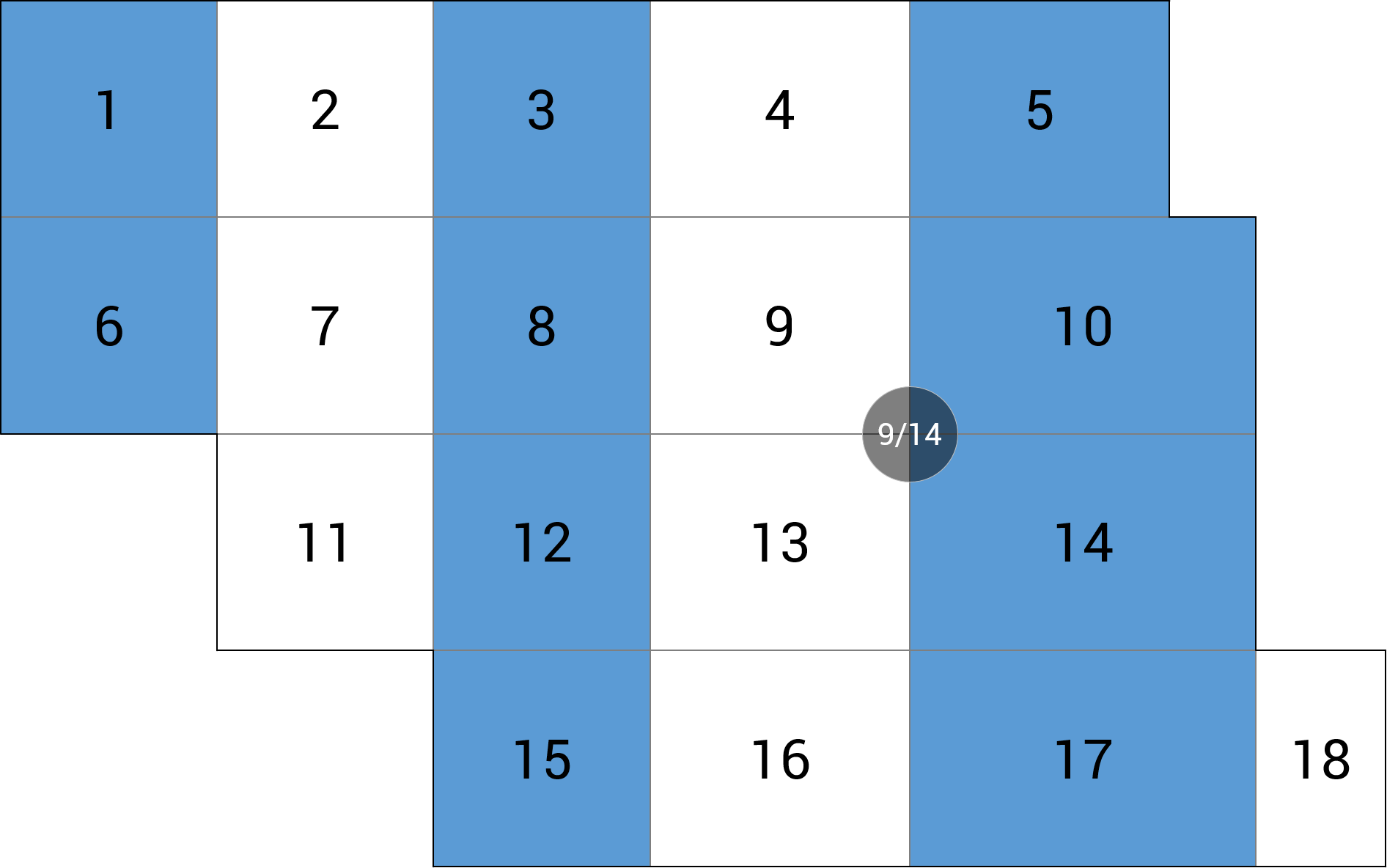 |
MY = -25.86 kNm (0.9%) |
Tab. 3b Schemat obciążeń i wyniki ugięć dla niezależnego rozkładu obciążeń
| Rozpatrywane miejsce | Schemat obciążenia | Ugięcie [mm] |
|---|---|---|
| a) przęsło wewnętrzne | (Jak dla mx) | -2.11 (-4.5%) |
| b) przęsło skrajne | (Jak dla mx) | -5.81 (-0.7%) |
| c) linia podpór |  |
-1.16(-4.9%) |
| d) podpora | 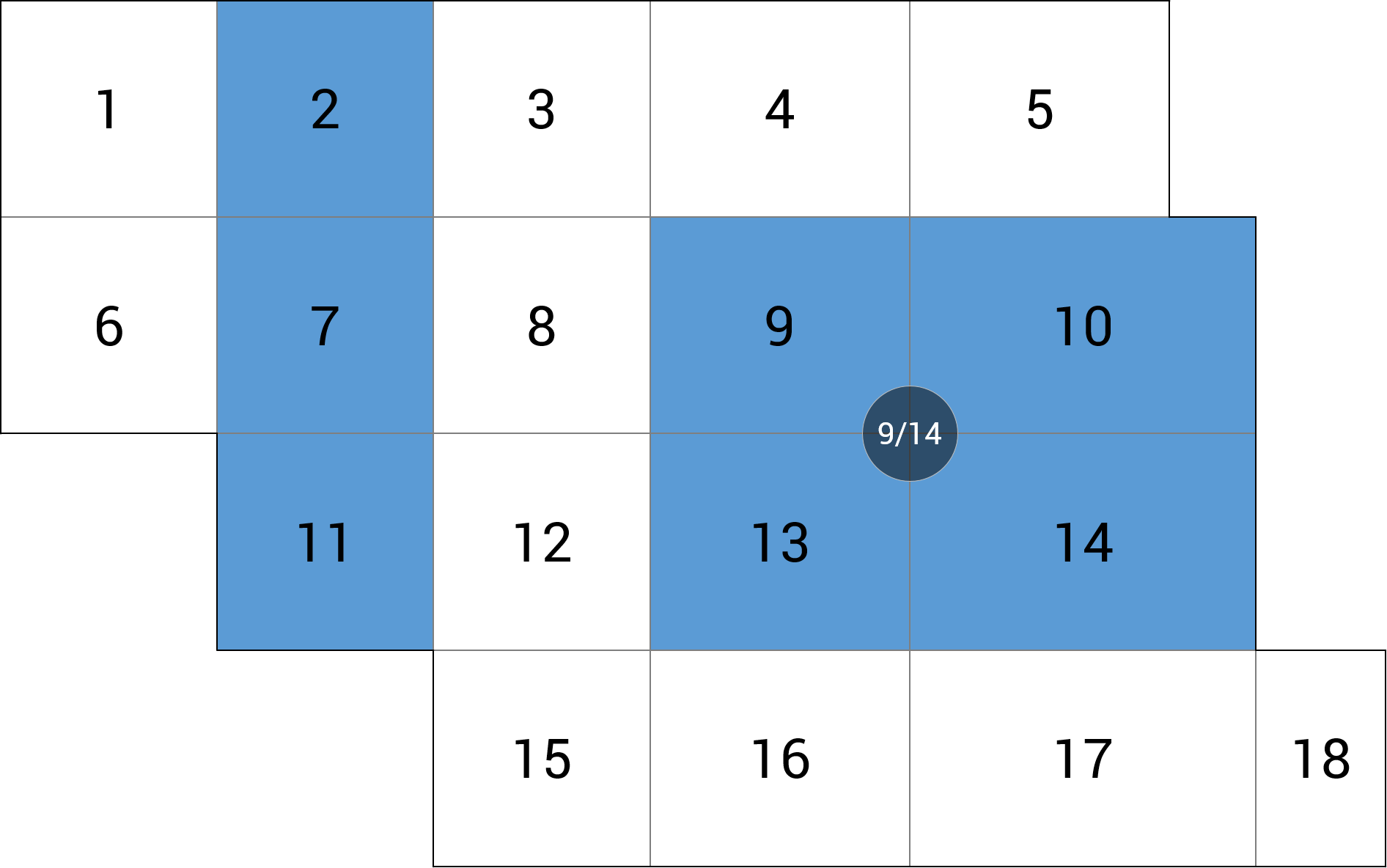 |
RZ = +206.6 kN (-1.2%) |
2. Schemat szachownicowy
Tab. 4a Schemat obciążeń i wyniki momentów zginających dla szachownicowego rozkładu obciążeń
| Rozpatrywane miejsce | Schemat obciążenia | Moment mx [kNm/m] |
|---|---|---|
| a) przęsło wewnętrzne |  |
+5.85 (-52.9%) |
| b) przęsło skrajne |  |
+11.71 (-46.3%) |
| c) linia podpór | 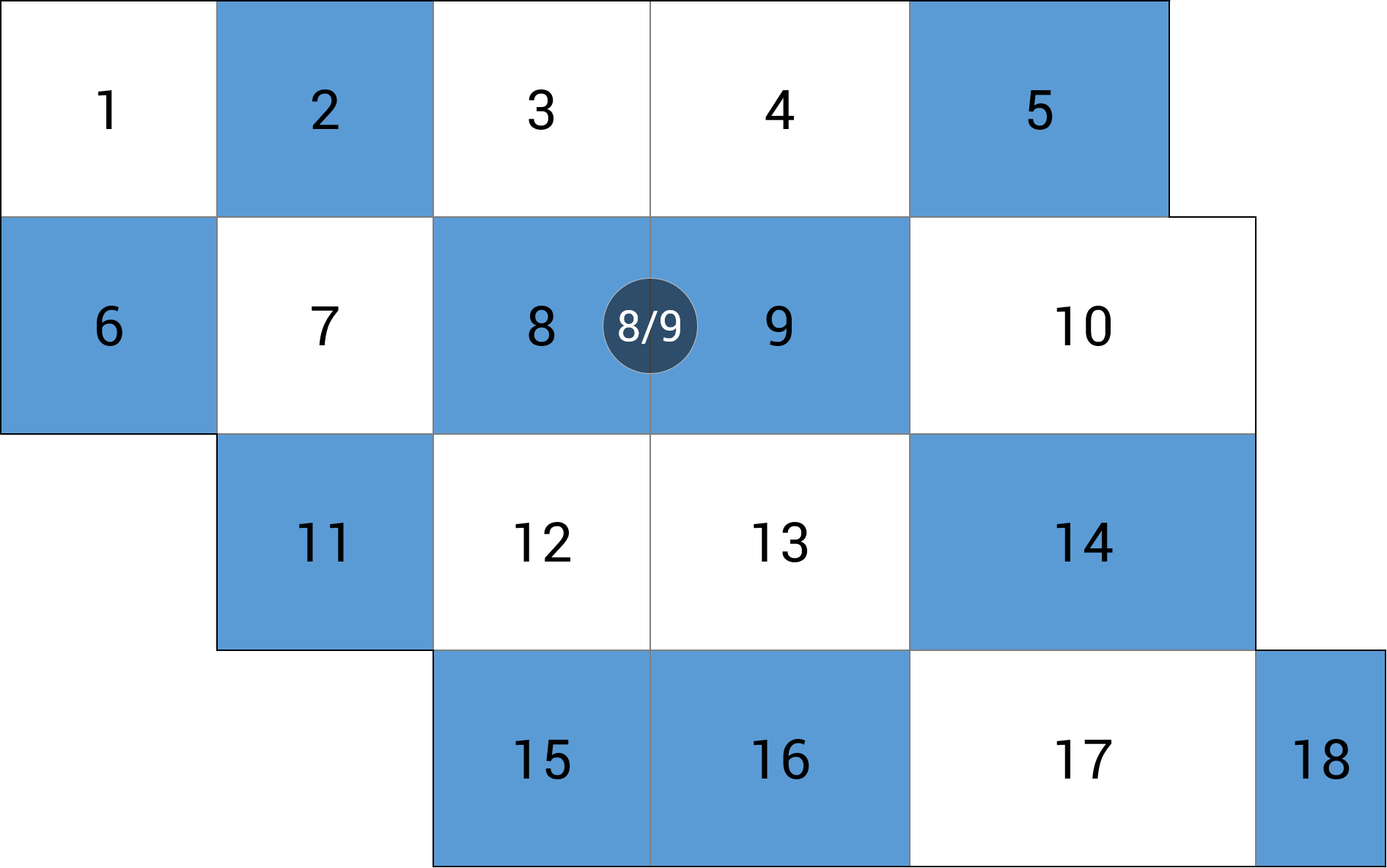 |
+0.23 (-102.8%) |
| d) podpora | 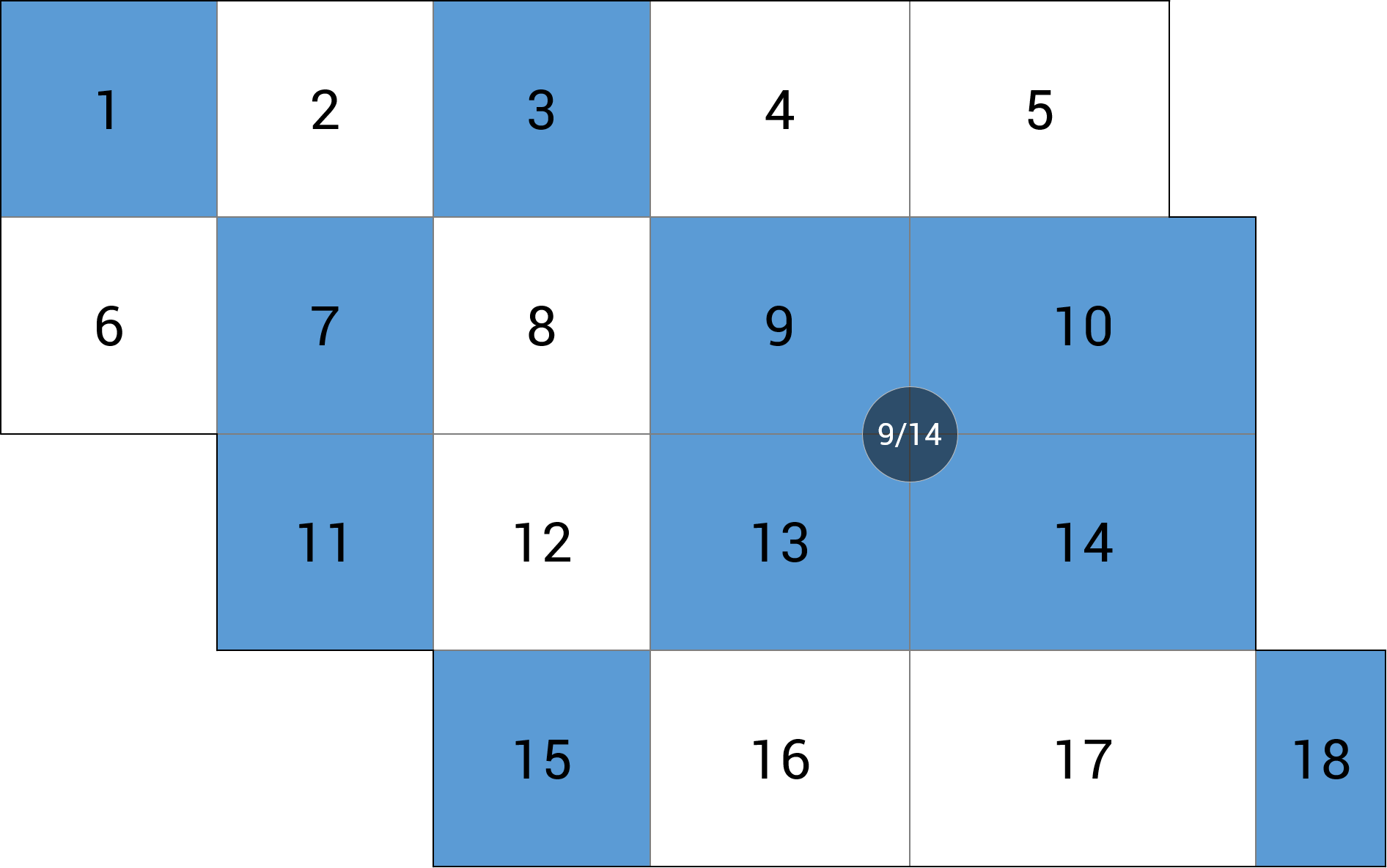 |
MY = -8.98 kNm (-65.0%) |
Tab. 4b Schemat obciążeń i wyniki ugięć dla szachownicowego rozkładu obciążeń
| Rozpatrywane miejsce | Schemat obciążenia | Ugięcie [mm] |
|---|---|---|
| a) przęsło wewnętrzne | (Jak dla mx) | -0.95 (-57.0%) |
| b) przęsło skrajne | (Jak dla mx) | -3.09 (-47.2%) |
| c) linia podpór | (Jak dla mx) | -1.03 (-15.6%) |
| d) podpora | (Jak dla MY) | RZ = +204.5 kN (-2.2%) |
3. Schemat pasmowy
Tab. 5a Schemat obciążeń i wyniki momentów zginających dla pasmowego rozkładu obciążeń
| Rozpatrywane miejsce | Schemat obciążenia | Moment mx [kNm/m] |
|---|---|---|
| a) przęsło wewnętrzne |  |
+12.53 (0.8%) |
| b) przęsło skrajne |  |
+21.59 (-1.0%) |
| c) linia podpór |  |
-5.55 (-33.4%) |
| d) podpora |  |
MY = -9.66 kNm (-62.3%) |
Tab. 5b Schemat obciążeń i wyniki ugięć dla pasmowego rozkładu obciążeń
| Rozpatrywane miejsce | Schemat obciążenia | Ugięcie [mm] |
|---|---|---|
| a) przęsło wewnętrzne | (Jak dla mx) | -2.11 (-4.5%) |
| b) przęsło skrajne | (Jak dla mx) | -5.81 (-0.7%) |
| c) linia podpór | (Jak dla mx) | -0.85 (-30.3%) |
| d) podpora | (Jak dla MY) | RZ = +191.4 kN (-8.5%) |
4. Obciążenie na całej powierzchni x Faktor = 1.20
Tab. 6a Schemat obciążeń i wyniki momentów zginających dla obciążenia na całej powierzchni stropu x Faktor = 1.20
| Rozpatrywane miejsce | Schemat obciążenia | Moment mx [kNm/m] |
|---|---|---|
| a) przęsło wewnętrzne |  |
+7.18 (-42.2%) |
| b) przęsło skrajne | (Jak dla a)) | +24.78 (4.9%) |
| c) linia podpór | (Jak dla a)) | -4.47 (-50.5%) |
| d) podpora | (Jak dla a)) | MY = -14.55 kNm (-47.6%) |
Tab. 6b Schemat obciążeń i wyniki ugięć dla obciążenia na całej powierzchni stropu x Faktor = 1.20
| Rozpatrywane miejsce | Schemat obciążenia | Ugięcie [mm] |
|---|---|---|
| a) przęsło wewnętrzne | (Jak dla mx) | -1.41 (-36.2%) |
| b) przęsło skrajne | (Jak dla mx) | -6.05 (3.4%) |
| c) linia podpór | (Jak dla mx) | -0.85 (-30.3%) |
| d) podpora | (Jak dla MY) | RZ = +222.1 kN (6.2%) |
5. Obciążenie na całej powierzchni x Faktor = 1.30
Tab. 7a Schemat obciążeń i wyniki momentów zginających dla obciążenia na całej powierzchni stropu x Faktor = 1.30
| Rozpatrywane miejsce | Schemat obciążenia | Moment mX [kNm/m] |
|---|---|---|
| a) przęsło wewnętrzne |  |
+7.78 (-37.4%) |
| b) przęsło skrajne | (Jak dla a)) | +24.78 (13.7%) |
| c) linia podpór | (Jak dla a)) | -4.47 (-46.3%) |
| d) podpora | (Jak dla a)) | MY = -14.55 kNm (-43.3%) |
Tab. 7b Schemat obciążeń i wyniki ugięć dla obciążenia na całej powierzchni stropu x Faktor = 1.30
| Rozpatrywane miejsce | Schemat obciążenia | Ugięcie [mm] |
|---|---|---|
| a) przęsło wewnętrzne | (Jak dla mx) | -1.53 (-30.8%) |
| b) przęsło skrajne | (Jak dla mx) | -6.55 (12.0%) |
| c) linia podpór | (Jak dla mx) | -0.92 (-24.6%) |
| d) podpora | (Jak dla MY) | RZ = +240.7 kN (15.1%) |

Zestawienie wyników
OK, mamy już zebrane wyniki wszystkich typowych schematów rozkładu obciążeń zmiennych. Spójrzmy teraz razem na ich wartości zebrane w jednej tabeli i oceńmy ich dokładność.
Tab. 8a Zestawienie odchyłek momentów zginających dla analizowanych schematów rozkładu obciążeń zmiennych (błąd w %)
| Schemat obciążeń | a) przęsło wewnętrzne | b) przęsło skrajne | c) linia podpór | d) podpora (MY) |
|---|---|---|---|---|
| Schemat niezależny | +0.8 | -0.6 | -31.7 | +0.9 |
| Schemat szachownicowy | -52.9 | -46.3 | -102.8 | -65.0 |
| Schemat pasmowy | +0.8 | -1.0 | -33.4 | -62.3 |
| Schemat na całej pow. x 1.20 | -42.2 | +4.9 | -50.5 | -47.6 |
| Schemat na całej pow. x 1.30 | -37.4 | +13.7 | -46.3 | -43.3 |
Tab. 8b Zestawienie odchyłek ugięć dla analizowanych schematów rozkładu obciążeń zmiennych (błąd w %)
| Schemat obciążeń | a) przęsło wewnętrzne | b) przęsło skrajne | c) linia podpór | d) podpora (RZ) |
|---|---|---|---|---|
| Schemat niezależny | -4.5 | -0.7 | -4.9 | -1.2 |
| Schemat szachownicowy | -57.0 | -47.2 | -15.6 | -2.2 |
| Schemat pasmowy | -4.5 | -0.7 | -30.3 | -8.5 |
| Schemat na całej pow. x 1.20 | -36.2 | +3.4 | -30.3 | +6.2 |
| Schemat na całej pow. x 1.30 | -30.8 | +12.0 | -24.6 | +15.1 |
Przejdźmy teraz kolejno po wynikach. Jak widać na pierwszy rzut oka, najmniejsze odchyłki – czyli wartości najbliższe rozwiązaniu dokładnemu – w tej analizie daje rozkład obciążeń zmiennych wg schematu obciążeń niezależnych oraz wg schematu pasmowego. Względne różnice w wartościach momentów zginających i ugięć dla tych schematów są zbliżone i nie przekraczają 5% w strefach przęsłowych (a i b). Sprawa komplikuje się w pozostałych miejscach.
Jeśli chodzi o wartości momentów zginających w linii podpór (c), to wyniki wykazują tam niedomiar względem rozwiązania dokładnego o ok. 33% – zarówno dla schematu niezależnego jak i pasmowego. Znaczący błąd wykazuje również moment podporowy (d) dla rozkładu pasmowego – niedomiar 62%, w odróżnieniu do schematu niezależnego, gdzie błąd wynosi poniżej 1%.
Analizując ugięcie w linii podpór dla schematu niezależnego widać, że błąd względny tego ugięcia wynosi poniżej 5%. Inaczej niż w schemacie pasmowym, gdzie analogiczne ugięcie obarczone jest błędem niedomiaru ponad 30%.
Podobna tendencja występuje w wynikach reakcji podporowych – schemat niezależny wykazuje wysoką zgodność z rozwiązaniem dokładnym (błąd poniżej 2%), natomiast schemat pasmowy daje nam błąd niedomiaru ok. 9%.
Zgodność wyników schematu niezależnego i rozwiązania dokładnego można uznać za zadowalającą. Jedynym wyjątkiem od tej reguły jest wartość momentu mx w linii podpór, gdzie błąd względny znacznie przekracza granicę 5% (dokładnie 32%). Dodatkowo, mimo swoich oczywistych zalet, schemat rozkładu niezależnych obciążeń zmiennych generuje – jak wspomniałem wcześniej – znaczną liczbę schematów obciążeń, równą co najmniej liczbie pól stropu. Wrócę jeszcze do tej sprawy we wnioskach.
Schemat szachownicowy w rozważanych przypadkach generuje niedopuszczalne różnice w wynikach w stosunku do rozwiązania dokładnego. I tak: błąd wartości momentów zginających we wszystkich analizowanych miejscach waha się w graniach 46% do 103% i są to wyłącznie błędy niedoszacowania (niedomiar).
Ugięcia stref przęsłowych wykazują błąd względny od 47% do 57% (odpowiednio dla przęsła skrajnego i wewnętrznego). Jest to również błąd niedoszacowania. Ugięcie w linii podpór wykazuje błąd najniższy ze wszystkich ugięć w tym schemacie na poziomie 16% niedomiaru. Jednak wartość momentu zginającego w tym miejscu obarczona jest błędem przekraczającym 100%. W dodatku znak działania momentu zginającego mx jest przeciwny względem rozwiązania dokładnego.
Jedynie wartość reakcji podporowej wykazuje zadowalającą zgodność z rozwiązaniem dokładnym – błąd ok. 2%. Błąd momentu podporowego wynosi jednak 65%.
Warte uwagi jest to, że zakładając pojedyncze obciążenie jedynie na analizowanym polu płyty dla uzyskania wartości maksymalnych momentów zginających i ugięć dla punktu w tym polu, błąd niedoszacowania jest znacznie mniejszy niż w schemacie szachownicowym (niedomiary: ok. 30% dla momentu mx i ugięcia w przęśle wewnętrznym oraz ok. 40% dla momentu mx i ugięcia w przęśle skrajnym).
Jeśli chodzi o schemat rozłożenia obciążenia zmiennego na całej powierzchni stropu z uwzględnieniem faktora zwiększającego (1.20 lub 1.30), to widać, że wyniki wyraźnie odbiegają od rozwiązania dokładnego. Wartości wyników dla przęsła wewnętrznego wykazują niedomiar grubo ponad 30% (faktor = 1.20: moment mx 42%, ugięcie 36%; faktor = 1.30: moment mx 37%, ugięcie 31%). Natomiast wyniki dla przęsła skrajnego wykazują dla odmiany mniejsze różnice błędu, w dodatku wszystkie po stronie bezpiecznej (faktor = 1.20: moment mx 5%, ugięcie 3%; faktor = 1.30: moment mx 14%, ugięcie 12%).
Wartość reakcji podporowej dla obu schematów jest naturalnie zawyżona, i tak dla faktora = 1.20 błąd względny wynosi ok. 6%, a dla faktora = 1.30 ok. 15%. Inaczej jest z momentem podporowym – w obu przypadkach wartości momentu są zaniżone o ok. 45%.
W tym miejscu możemy pokusić się o końcowe wnioski. Jednak nie poddawajmy się tak szybko. Spróbuję jeszcze pokazać wam dwie alternatywne metody rozkładu obciążeń: schemat obciążenia co 2. pole oraz schemat obciążenia co 3. pole. Są to schematy, które po pierwsze: będą mniej pracochłonne od tych przedstawionych powyżej, i po drugie: ich dokładność będzie podobna tej otrzymanej z rozkładu obciążeń wg schematu niezależnego. Zrobię to jednak już w następnym wpisie, z tej racji, że ten tekst ma już sporą długość, a chciałbym dać wam też możliwość na przyjrzenie się tematowi na spokojnie.
Wnioski
Uff, sporo tego było. Teraz spróbuję podsumować, to udało się nam zrobić.
Dowiedzieliśmy się w jaki sposób należy rozkładać obciążenia zmienne na stropie na podstawie analizy powierzchni wpływu. Przetestowaliśmy 5 różnych sposobów rozkładu obciążeń zmiennych, porównaliśmy je z rozwiązaniem dokładnym opartym na powierzchniach wpływu i określiliśmy wady i zalety każdego z nich.
Przede wszystkim przedstawione przykłady pokazują nam jak ważne jest odpowiednie (tj. miarodajne) rozłożenie obciążeń zmiennych w ustrojach płytowo-słupowych. Nie każdy schemat nadaje się do zastosowania dla ustrojów płytowo-słupowych (np. schemat szachownicowy), niektóre nadają się jedynie w ograniczonym zakresie (schemat pasmowy w obszarach przęsłowych). Dlatego, jeśli nie mamy pewności, zalecam przed rozłożeniem obciążeń zmiennych analizę przebiegu powierzchni wpływu do określenia właściwego rozkładu obciążeń (np. sprawdzenie konieczności dzielenia obszarów pól o stosunkowo dużych wartościach obciążeń na obszary mniejsze).
(1) Niezależny schemat rozkładu obciążeń zmiennych na poszczególnych polach stropu można uznać za najskuteczniejszy do uzyskania wiarygodnych obwiedni sił wewnętrznych i ugięć (granica błędu zwykle do 5%). Jedyna znacząca różnica w wynikach – w porównaniu do rozwiązania dokładnego – występuje w wartości momentu zginającego w linii podpór (błąd niedomiaru 32%). Oczywiście nie można tego bagatelizować. Z drugiej jednak strony taki mikro-podział obciążenia zmiennego jak w przypadku powierzchni wpływu nie jest praktycznie możliwy w rzeczywistości, a prawdopodobieństwo rozkładu obciążeń zmiennych w naturze dokładnie wg przebiegu powierzchni wpływu jest niewielkie. Dodatkowo, istotny udział obciążeń stałych w obwiedni sił i ugięć powoduje zacieranie się tych różnic. Prawda zatem leży gdzieś pośrodku…
Moim zdaniem rozkład obciążeń zmiennych wg schematu niezależnego na stropach płytowo-słupowych jest miarodajny. Należy przy tym tylko pamiętać o możliwości niedoszacowania momentów zginających w pasmach słupowych. Najczęściej jednak schemat ten, z racji liczby przypadków obciążeń, jest dość pracochłonny, zwłaszcza przy większej licznie pól obciążeń.
(2) Stosowanie schematu szachownicowego dla ustrojów płytowo-słupowych jest niedopuszczalne – względne błędy niedoszacowania przekraczają 45%. Uwzględniając nawet wszystkie korzystne zjawiska, jak wielkość stropu czy udział obciążeń stałych w obwiedni, nie można go uznać za miarodajny w odniesieniu do ustrojów płytowo-słupowych.
(3) Schemat pasmowy uznać można za miarodajny dla wielości poszukiwanych jedynie w przęśle (zwykle błąd niedomiaru poniżej 5%). Nie dotyczy to wielkości w linii podpór, gdzie błąd względny wzrasta i przekracza 30% (tutaj niedomiar zarówno do momentu zginającego jak i ugięcia). Dodatkowo wyraźnie zaniża on wartość momentu podporowego, nawet o 62%. Schemat ten, mimo swojej prostoty, jest rozwiązaniem czasochłonnym oraz ograniczonym co do możliwości wariantowania wyników w stosunku do schematu niezależnego, zwłaszcza jeśli obliczenia prowadzimy programami MES.
(4 i 5) Wielokrotne schematy obciążeń niezależnych o rozkładzie co 2. lub co 3. pole wydają się być skutecznym sposobem rozkładu obciążeń zmiennych. Są to sposoby, których wyniki obliczeń nie odbiegają znacząco od rozwiązania dokładnego i są w większości zbliżone do wyników ze schematu niezależnego.
Podsumowanie
Na bazie przeprowadzonej analizy porównawczej rozkładu obciążeń zmiennych na stropie płytowo-słupowym możemy spróbować to teraz jak najtreściwiej podsumować.
Najdokładniejszym z typowych sposobów rozkładu obciążeń zmiennych na stropie typu płyta-słup jest schemat obciążeń niezależnych. Generuje on miarodajne wyniki momentów zginających, ugięć i reakcji podporowych w odniesieniu do rozwiązania dokładnego opartego na powierzchniach wpływu.
Na koniec kilka uwag ogólnych:
- Jak się domyślacie – im większa powierzchnia stropu, tym błędy w rozkładzie obciążeń zmiennych względem rozwiązania dokładnego zacierają się. Co nie oznacza oczywiście, że mogą całkowicie zaniknąć (por. schemat szachownicowy). W swojej pracy magisterskiej przeanalizowałem strop płytowo-słupowy o 38 polach obciążeń i różnice wyników dla schematu niezależnego nie przekraczały tam błędu 5% względem rozwiązania dokładnego,
- Dodatkowo – jak wspomniałem podsumowując wyniki schematu niezależnego – udział obciążeń stałych w obwiedni sił i ugięć jest zazwyczaj na tyle istotny, że różnice pomiędzy rozwiązaniem dokładnym a innymi schematami rozkładu obciążeń zmniejszają się,
- Jak widać dokładność wyników na poziomie 5% jest bardzo ostrym kryterium, nawet dla takiego schematu obciążeń jak rozkład niezależny. Nie przez przypadek taki właśnie próg błędu ustaliłem tutaj. Chciałem wam zasygnalizować, że projektowanie w codziennej praktyce – jak to kiedyś usłyszałem od prof. Starosolskiego – jest bardziej szacowaniem aniżeli analizą. Oczywiście nie twierdzę tutaj, że 5% jest błędem i należy podchodzić do wyników z większą swobodą ;) Chcę za to dać do myślenia, że decyzja ostatecznie należy do projektanta, do każdego z nas,
- Przy rozległych stropach warto by się zastanowić nad alternatywnym sposobem rozkładu obciążeń zmiennych – takim, który znacznie zmniejsza nakład pracy i jednocześnie zapewnia miarodajne wyniki obliczeń. Taką analizę zasygnalizowałem przy komentarzu wyników. W następnym wpisie z tego cyklu opracuję to szczegółowo.
OK, a co wy o tym myślicie? Sporo było analizowania, ale myślę, że udało mi się wskazać konkretne i bezpieczne metody rozkładu obciążeń zmiennych (czytaj: schemat obciążeń niezależnych). Jeśli macie pytania, piszcie śmiało w komentarzach. Chętnie poznam wasze spojrzenie na ten temat.
Wpisy z cyklu „Rozkład obciążeń zmiennych„:
- Powierzchnie wpływu,
- Strop płytowo-słupowy,
- Strop płytowo-słupowy – metody alternatywne,
- Strop płytowo-belkowy,
- Strop oparty na ścianach (w opracowaniu).
Źródła
- Starosolski W., Aneks do: Wybrane zagadnienia komputerowego modelowania konstrukcji inżynierskich, na prawach rękopisu, Pro-Soft, Gliwice 2007,
- Starosolski W., Komputerowe modelowanie betonowych ustrojów inżynierskich. Wybrane zagadnienia, t.1 i 2, Wyd. Politechniki Śląskiej, Gliwice 2009,
- Starosolski W., O rozmieszczeniu obciążeń zmiennych w stropach krzyżowo zbrojonych i płytowo-słupowych, Inżynieria i Budownictwo, nr 4/2008,
- Starosloski W., Projektowanie płytowo-słupowych ustrojów żelbetowych i sprężonych wg Euro-Norm, PRO-SOFT, Gliwice 2010,
- Starosolski W., Wybrane zagadnienia komputerowego modelowania konstrukcji inżynierskich, Wyd. Politechniki Śląskiej, Gliwice 2003,
- Zdanowicz Ł., Praca magisterska: Analiza obliczeniowa i projekt konstrukcji wielokondygnacyjnego budynku o ustroju płytowo-słupowym, Kraków 2010.

Cześć chciałem tylko powiedzieć, że strona bardzo długo wczytuje
się.
Dzięki za info. Przyjrzę się temu.
Bardzo wartościowa (dla mnie) analiza.
Analiza która odnosi się do konkretnego schematu i nie powinno się jej w prost przenosić na resztę układów. Myślę że ogromne znaczenie mają też proporcje siatki słupów.
Nie mniej daje do myślenia w metodologii projektowania bezkrytycznie przyjmowanej niestety przez wielu. Myślę że nie pomyliłbym się mocno gdybym powiedział że większość przyjmuje schemat szachownicowy dla takiego układu.
Dzięki Andrzej za dobre słowo! Racja, racja trzeba być czujnym przy innej geometrii (rozpiętości słupów etc.). Trzeba też jednak szukać bardziej ogólnych metod, bardziej uniwersalnych. Tak np. w tego typach stropach zazwyczaj rozkładam obciążenie zmienne wg podejścia co 3. pole. Jestem świadom odchyłek, ale też obliczenia idą szybciej.
Co do schematu szachownicowego, to tutaj tylko unikać jak ognia. Mam jednak nadzieję, że coraz mniej projektantów używa go w obliczeniach tego typu płytach.
Czy pomysł użycia współczynnika zwiększającego pochodzi z normy/ książki/ artykułu? Piszę pracę dyplomową na temat ustrojów płytowo- słupowych, jednak w żadnych publikacjach nie widziałam zapisu o stosowaniu współczynników zwiększających (jedynie o nich słyszałam). Czy jest Pan w stanie podać mi źródło tego zapisu. Z góry bardzo dziękuję za pomoc
Cześć! Jeśli chodzi o schemat ze współczynnikiem zwiększającym, to niestety nie mam źródeł do wskazania. Stosuje to jednak wielu projektantów (bardzo szybki sposób). Dość łatwo wyjaśnić tą metodę na podstawie porównania do typowej obwiedni np. momentów – faktor ma na celu zwiększenie momentów w prześle i nad podporą tak, żeby wyniki były zbliżone do tych otrzymanych z obwiedni. Dobry szkic powinien wszystko wyjaśnić :)
Powodzenia w pisaniu pracy! Płyta-słup to ciekawe ustroje.