W projektowaniu często zakładamy pewne mniej lub bardziej uzasadnione uproszczenia w celu obliczenia poszczególnych elementów konstrukcji, jak stropy itp. Jednym z nich jest poprawne zdefiniowanie warunków brzegowych, czyli podpór konstrukcji.
Może nieraz zastanawiacie się czy uwzględnianie podatności słupów czy ścian przy wymiarowaniu stropu ma sens? A jeśli już ma, to jaki ma to wpływ na wyniki obliczeń?
W tym tekście przedstawię Wam jakie są skutki stosowania podpór sztywnych i podatnych w projektowaniu stropu. Pokażę również jak prosto określić sztywności zastępcze podpór takie jak słupy czy ściany.
Przy tej okazji przygotowałem też dla Was prezent! Na potrzeby tego artykułu stworzyłem kalkulator do określenia zastępczych sztywności podpór. Link znajduje się na końcu tekstu.
Kiedy uwzględnienie podatności podpór ma sens?
Generalnie jest kilka sytuacji, kiedy uwzględnienie podatności podpór ma istotne znaczenie. Są to m.in.:
- podpory z materiałów o znacznej różnicy sztywności – np. beton, stal, mur,
- podpory o zróżnicowanych przekrojach poprzecznych (np. występowanie w jedym układzie słupów wiotkich i krępych lub mieszanka słupów i ścian),
- konstrukcje o zróżnicowanym osiadaniu fundamentów,
- odwzorowanie właściwej pracy naroży i końców ścian (ryzyko powstania sztucznego momentu zamocowania).
We wszystkich tych sytuacjach występuje spore ryzyko błędnych wyników przy obliczeniu stropów lub belek opartych na sztywnych podporach (np. reakcji podporowych i sił wewnętrznych). W rzeczywistości każda podpora jest – mniej lub bardziej – podatna, co wpływa bezpośrednio na rozkład sił w konstrukcji.
Weźmy prosty przykład – strop oparty na ścianach, gdzie jeden narożnik płyty jest podpierany przez naroże ściany (por. rysunek poniżej).
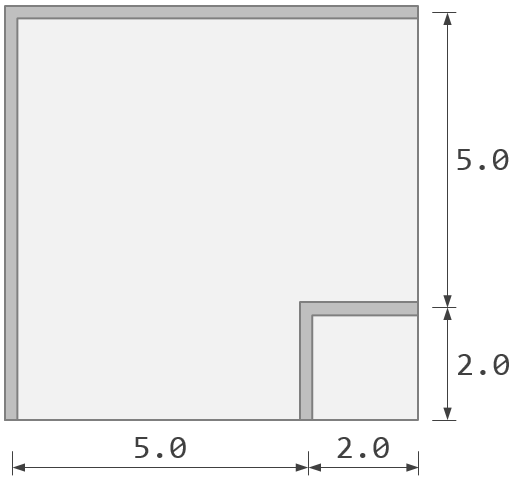
Rys. 1 Geoemtria stropu
Dane modelu: beton C25/30, rozpiętość stropu: B/L = 7.0/7.0 m, wysokość kondygnacji: H = 3.5 m, grubość stropu: h = 0.20 m, grubość ścian: hs = 0.20 m, obciążenie qk = 10.0 kN/m2.
Przeanalizujemy 2 warianty:
- wariant (1) – płyta oparta na ścianach niepodatnych (podpory sztywne),
- wariant (2) – płyta oparta na ścianach z uwzględnieniem ich podatności.
(Sposób określenia zastępczej sztywności ściany opiszę dokładnie w drugiej części tekstu). Wyniki obu wariantów wyglądają następująco:
Wyniki dla obu wariantów (1) i (2)
| Parametr | Wariant (1) Podpora sztywna | Wariant (2) Podapora podatna | (1)/(2) |
|---|---|---|---|
| Max reakcja podporowa – naroże [kN/m] | 1607 | 820 | 196% |
| Wartość średnia reakcji – naroże [kN/m] | 185.6 | 134.8 | 138% |
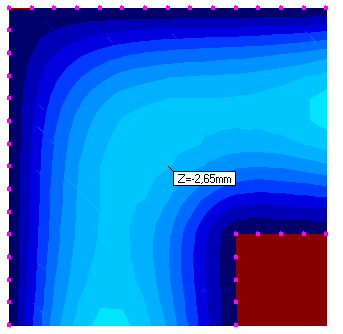
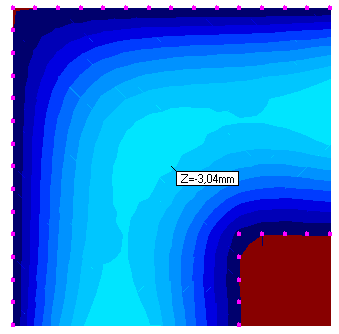
| Ugięcie w środku przęsła [mm] | 2.65 | 3.04 | 87% |
Jak pokazują wyniki obliczeń nieuwzględnienie podatności ścian powoduje lokalnie prawie 2-krotne zawyżenie reakcji podporowej względem podpory z uwzględnioną podatnością. Przy sztywnym połączeniu, niemal cała reakcja stropu jest skoncentrowana na niewielkim odcinku w obszarze naroża, co nie odpowiada rzeczywistej pracy podpory (por. rys.2).
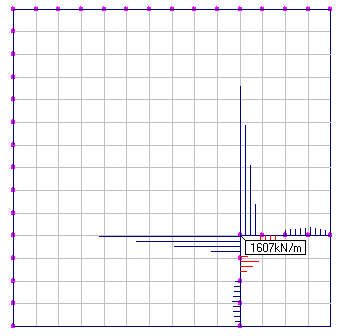 |
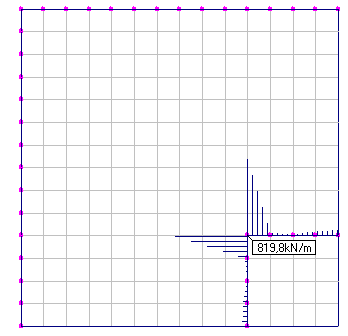 |
|---|---|
| Podparcie sztywne | Podparcie podatne |
Rys. 2 Reakcje podporowe stropu – podparcie sztywne (po lewej/góra), podparcie podatne (po prawej/dół)
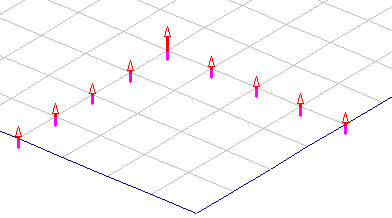
Dodatkowo, tuż za tym spiętrzeniem reakcji występuje reakcja o znaku przeciwnym do spodziewanego (dodatkowy moment utwierdzenia). W przypadku podpory podatnej przebieg reakcji jest zgodny z intuicją – por. rys.3. Średnia wartość reakcji podporowych na analizowanym odcinku ściany różni się pomiędzy wariantami (1) i (2) o 38%.
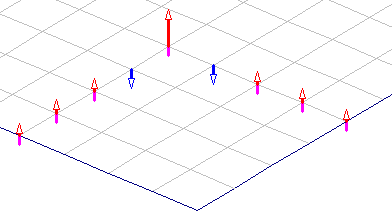 |
 |
|---|---|
| Podparcie sztywne | Podparcie podatne |
Rys. 3 Reakcje podporowe stropu w ujęciu wektorowym – podparcie sztywne (po lewej/góra), podparcie podatne (po prawej/dół)
Jeśli spojrzymy na ugięcia płyty na rys.4, to okazuje się, że wartość maksymalnego ugięcia w środku pola stropu jest mniejsza dla modelu z podporami sztywnymi (u = 2.65 mm) w porównaniu od modelu z podporami podatnymi (u = 3.04 mm). Względna rożnica ugięć pomiędzy wariantem (1) i (2) wynosi 100% – 87% = 13%. Powodem zaniżenia wartości ugięcia płyty opartej na ścianach sztywnych jest dodatkowy moment utwierdzenia powstały w narożu ściany, który „podnosi” przęsło płyty.
 |
 |
|---|---|
| Podparcie sztywne | Podparcie podatne |
Rys. 4 Ugięcie stropu – podparcie sztywne (po lewej/góra), podparcie podatne (po prawej/dół)
Ten prosty przykład pokazuje jak duże znaczenie ma rzeczywiste odwzorowanie warunków brzegowych stropów.

Przejdźmy teraz do sposobu określenia sztywności zastępczej podpory.
Sztywnosć zastępcza podpory
Aby określić zastępczą sztywność podpory i uzyskać bardziej rzeczywiste wyniki sił wewnętrznych i reakcji podporowych należy uwzględnić parametry tej podpory. Są to:
- geometria przekroju podpory,
- rodzaj materiału podpory,
- długość elementu podpierającego (podpory).
W zależności od kierunku działania podpory rozróżnia się kilka rodzajów sztywności. Najczęściej spotykane i wykorzystywane w praktyce projektowej to:
- sztywność podłużna (kierunek względem osi Z) – współczynnik kZ,
- sztywność obrotowa (kierunek X i Y) – współczynniki kX i kY.
Interpretacja fizyczna współczynnika kZ [kN/m] mówi o tym jaka siła konieczna jest do uzyskania jednostkowego przemieszczenia elementu. Podobnie jest dla współczynników kX i kY – dotyczą jednostkowego obrotu węzła.
Współczynniki kZ, kX i kY możemy odpowiednio określić dla słupa lub ściany i są obliczane na podstawie poniższych wzorów. Równania te oparte zostały na wzrorach transormacyjnych metody przemiszczeń.
Podatność słupa
Podatność podłużna:
![]()
Podatność na obrót:
![]()
![]()
gdzie: ![]() – moduł sprężystości materiału podpory [GPa],
– moduł sprężystości materiału podpory [GPa], ![]() – pole powierzchni przekroju poprzecznego podpory [m2],
– pole powierzchni przekroju poprzecznego podpory [m2], ![]() – długość podpory (zwykle wysokość kondygnacji) [m],
– długość podpory (zwykle wysokość kondygnacji) [m], ![]() – moment bezwładności przekroju podpory względem osi X i Y,
– moment bezwładności przekroju podpory względem osi X i Y, ![]() – zakłada się
– zakłada się ![]() = 3, kiedy koniec podpory jest zamocowany przegubowo;
= 3, kiedy koniec podpory jest zamocowany przegubowo; ![]() = 4 – kiedy koniec podpory jest zamocowany w pełni (utwierdzony) – por. rys.5.
= 4 – kiedy koniec podpory jest zamocowany w pełni (utwierdzony) – por. rys.5.
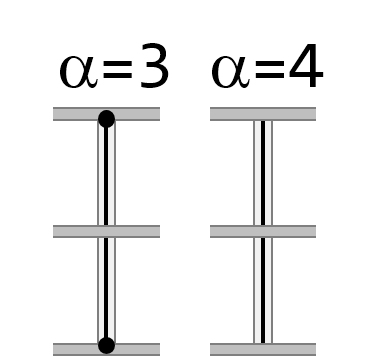
Rys. 5 Interpretacja współczynnika ![]() – połączenie przegubowe (po lewej), połączenie sztywne (po prawej)
– połączenie przegubowe (po lewej), połączenie sztywne (po prawej)
Uwaga: W przypadku stropu, w którym istnieje dodatkowo słup górny (nad stropem), wartości kX (lub kY) sumujemy (np. ![]() ).
).
Podatność ściany
Podatność podłużna:
![]()
Podatność na obrót:
![]()
gdzie: ![]() – jw.,
– jw., ![]() – pole powierzchni przekroju poprzecznego na 1 mb ściany [m2/mb],
– pole powierzchni przekroju poprzecznego na 1 mb ściany [m2/mb], ![]() – jw.,
– jw., ![]() – moment bezwładności przekroju na 1mb ściany względem osi X [m3/mb],
– moment bezwładności przekroju na 1mb ściany względem osi X [m3/mb], ![]() – jw.
– jw.
Uwaga: W przypadku stropu, w którym istnieje dodatkowo ściana na górze (nad stropem) wartości kX sumujemy (![]() ).
).
Wzory te można stosować zarówno do podpór żelbetowych, murowych czy stalowych. Należy jedynie podstawić odpowiednie wartości modułu Younga.
Przykład obliczeniowy
Przetrenujmy teraz na konkretnym przykładzie stropu podpartego słupami żelbetowymi.
Dane
Słup dolny, połączony ze stropem monolitycznie:
- b = 0.30 m
- h = 0.40 m
- L = 3.00 m
- Ec = 32.0 GPa (beton C30/37)
Słupa górny – brak
Obliczenia
![]()
![]()
![]()
Sztywności zastępcze podpór:
![]()
![]()
![]()
![]()
![]()
Na koniec mały prezent :)
Jak widzicie, dzięki podanym wzorom jesteście w stanie określić sztywność zastępczą podpór stropu. Wzory są proste i uniwersalne.
Na koniec przygotowałem dla Was prezent! Na potrzeby tego artykułu stworzyłem kalkulator do określenia zastępczych sztywności słupów i ścian. Dodatkowo, rozbudowałem go o opcję częściowego zamocowania w przedziale 0% (przegub) do 100% (utwierdzenie). Plik możecie ściągnąć pod tym linkiem. Miłego korzystania!
Z pozdrowieniami,




Rozumiem, że jeżeli w programie mogę zadać podporę powierzchniową, gdzie wymagane jest podanie podatności w MN/m3, wystarczy, że podzielę moduł Younga przez wysokość ściany/słupa?
O’K, dzięki, a coś na temat podatności podparcia belki na podciągu lub wsporniku?
—
Pozdrowienia
St. Plechawski
Co do belki czy podciągu, to już opracowanie tego w prosty kalkulator nie jest takie łatwe ;) Najłatwiej to zrobić model 3d.
„Rys. 5 Interpretacja współczynnika – podparcie sztywne (po lewej/góra), podparcie podatne (po prawej/dół)” – no nie rozumiem o co chodzi z tym „po lewej/góra” i ” po prawej/dół” jak również tego, czym jest „koniec podpory”. Czy mogę prosić o wyjaśnienie doboru współczynnika alfa? – jakieś materiały źródłowe?
Dzięki za czujność! Już poprawiłem opis. Chodziło o połączenie sztywne (rys. po lewej) i przegubowe (rys. po prawej). Co do szczegółów, to polecam pobrać plik Excel do wyznaczania sztywności podpór – tam można wszystko podejrzeć (formuły są widzoczne) :) Link do strony zapisu tutaj: https://oprojektowaniu.pl/newsletter/
Hmm, ale rysunek z lewej wygląda jak przegubowy, a z prawej jak utwierdzony i tak też sugerują wartości alfa – czy się mylę?
Poprawione, a Ty masz u mnie kawę :)
Dzień dobry,
bardzo przydatny artykuł. Mam pytanie odnośnie zadawania podatności dla ścian murowanych. W programach inżynierskich często z góry podatność możemy podać jedynie w jednostce kN/mm. Skorzystałem z kalkulatora, który Pan zamieścił i po przeliczeniu dla: modułu Younga 7,0 GPa, grubości 24 cm, wysokości 3,00 m i przegubie (0%) podatność wyniosła 560 000 kN/m/m, czy w tym wypadku wartość w programie będzie wynosiła 560 kN/mm, czy 56 kN/mm? Chodzi o rząd wielkości, już nawet nie o ten konkretny przypadek, czy z doświadczenia jest Pan w stanie sprecyzować wartość dla ścian murowanych (zdaję sobie sprawę, że rozrzut jest duży z uwagi na różnorodność materiałów).
Wartość 560 000 kN/m/m odpowiada 560 kN/m/mm. Zadając podatność podpory w postaci ściany musi być tutaj miano siła / metr bieżący / przemieszczenie. Wartość dla ściany powinna mieć w programie podobne jednostki. Jednostki typu kN/mm to podatność podpory skupionej (słupa).
Super artykuł:) Mam takie pytanko jeszcze, bo być może tego nie wyłapałam dobrze, ale w jaki sposób określić sposób zamocowania od 0 do 100 %, tak żeby miało to odzwierciedlenie w rzeczywistości ?
Tutaj jest to funkcja stosunku sztywności stropu i podpory. Im masywniejszy strop w porównaniu do podpory, to tym wyższy stopień utwierdzenia. Ten faktor przyjmowany jest na podstawie doświadczenia. Rekomenduję przyjmować 0, to obliczać stropy jako podparte przegubowo. Masz wtedy zapas nośności w stropie.
Ok, połączenie przegubowe będzie korzystne(konserwatywne) dla obliczeń stropu, ale już nie dla ściany. Norma EC6 w zał. C pokazuje jak obliczyć moment węzła strop-sciana, ale to metoda analityczna. Jak byś przyjmował sztywność węzła strop-ściana murowana w modelu MES żeby mieć moment zginający, ale żeby nie był on przesadzony? (Zbyt duże momenty to bolączna sztywnych połączeń paneli, nie uwzględnia to częściowego zamocowania i redukcji sztywności z uwagi na zarysowanie)
Dzięki!
Dzięki za komentarz. Połączenie stropu ze ścianą murowaną jest fikcyjne i nie możemy tutaj mówić o węźle. Jest to po prostu oparcie stropu na ścianę, gdzie momenty ze stropu nie przekazują się na ścianę (nie ma takiej możliwości). Moment, o którym mówisz bierze się mimośrodowego przyłożenia reakcji podporowej. Są to dwie różne rzeczy.
Moim zdaniem modelowanie połączenia stropu ze ścianą, aby przenosić momenty nie ma do końca sensu praktycznego.
Na pewno? W przypadku oparcia stropu na calej szerokości sciany geometrycznie nie ma mimosrodu, wynika on glownie z momentu zginajacego. Zgadzam sie że momenty zginające przekrój ściany nie mogą przekazywac sie na strop. Z 2giej strony mimośrode obciążenie sciany jest wynikiem momentu (e=M/N). Jestem ciekawy czy masz jakiś sposób jak w modelu MES budynku uzyskać momenty zginające dzialajace na ścianę, a jednoczesnie nie dodawac sztucznych momentów w stropie. Myslalem o tym zeby robic 2 modele: 1 do wymiarowania stropu, gdzie połączenie ze sciana jest przegubowe, a 2gi model do wymiarowania scian, gdzie polaczenie scian i stropu jest podatne, zeby uzyskac mkmwnty zginające ścianę ( zbieznej wielkosci z tymi uzyskamymi megodą z EC6 zał. C.
Zazwyczaj wymiarując płytę stropu zadaje sie przeguby na polaczeniu strop-sciana i dostaje sie momenty zginające w scianie rowne 0, a to nie jest prawda. Mimośrody w scianie pochodza m.in od momentu zginającego (e=M/N) wiec bez uwzglednienia momentu, ktory wynika z obciazenia stropu i ze sztywnosci elementów dochodzacych, sciana bedzie niedowymiarowana. Drobiec pisal o przykladach awarii scian zewnętrznych, gdize nie uwzględniono tego ze obciazenie stropu generuje moment zginajacy w scianie.
Chyba że się mylę i źle do tego wszystkiego podchodzę ;)
Co do momentów w ścianie przy oparciu na ścianie murowanej, to moment ten jest wynikiem mimośrodu przyłożenia reakcji, a nie odwrotnie. To rozróżnienie jest ważne. Momenty w ścianie murowanej otrzymasz po uwzględnieniu procedury Eurokodu, która opisuje to dokładnie ( M = N x e). Nota bene w zał C przyjęta sprężystość, co dla murów stanowi spore uproszczenie.
Tworzenie dwóch modeli – moim zdaniem – nie ma żadnego sensu. Najlepiej, jak zrobisz kilka testów z różnymi konfiguracjami i zobaczysz jak różnią się wyniki. Wtedy będziesz wiedzieć, gdzie masz zapasy, a gdzie niedoszacowania. Pozwoli Ci to też wybrać jeden model, który jest najsensowniejszy – poeksperymentuj :)
witam, wiesz moze jak policzyc sztywnosć zamocowania stopy fundamentowej w podlozu gruntowym? chodzi o wartośc podana w kNm/rad (kNm/deg)
Są na to wzory – zerknij na str. 22 w: https://www.frilo.eu/files/_inhalte/downloads/de/pdf_doku_archiv/B5.pdf (po niemiecku)
dobry artykuł. opisany prosto zrozumiale, z interpretacją fizyczną – takie zdania w dużym stopniu ułatwiają zrozumienie tematu (przynajmniej dla mnie). Dzięki
Dzięki za opinię! Dla mnie kluczowe jest to, żeby treści rzeczywiście uczyły :)