Sztywność pala w gruncie

Sztywność pala w gruncie jako podpora zastępcza

20 lipca 2017

Projektujesz płytę fundamentową, ale nie wiesz jaką sztywność mają pod nią pale? Dostałeś wyniki badań geotechnicznych gruntu, ale nie wiesz jak z nich skorzystać? Szukasz prostego sposobu na to jak określić sztywność pala fundamentowego w gruncie jako podporę zastępczą? Dowiedz się jak sobie z tym poradzić.

W projektowaniu konstrukcji bardzo często zdarza się, jeszcze zanim zaczniemy dokładnie analizować posadowienie, że musimy założyć konkretne warunki brzegowe (podparcie) modelu konstrukcji. O ile modelujemy np. strop 3-ciej kondygnacji naziemnej, to nie ma problemu – podpory wynikają ze sztywności elementów znajdujących się bezpośrednio pod nią, jak słupy czy ściany. Problem pojawia się wtedy, kiedy obliczamy np. płytę fundamentową czy model całej konstrukcji (3D) posadowionych na palach fundamentowych. Jakie warunki podporowe wtedy założyć? Jaką sztywność zastępczą mają pale?

W tym wpisie przedstawię Wam uproszczoną metodę na określenie sztywności zastępczej pojedynczego pala na podstawie informacji, jakie zwykle posiadamy.

Jak pracuje pal fundamentowy?

Pale fundamentowe, mimo swoich różnic, spełniają tą samą funkcję – przenoszą bezpiecznie obciążenia z konstrukcji na grunt. Ich praca też wygląda podobnie. Poniżej na rysunku pokazałem jak pracuje typowy pal fundamentowy. Z racji swojej geometrii, przenosi on obciążenia bezpośrednio na grunt poprzez swoją podstawę jak i swoją pobocznicę. Nośność pojedynczego pala jest to suma nośności tych składowych: – nośności podstawy pala (R_b) oraz – jego pobocznicy (R_s).

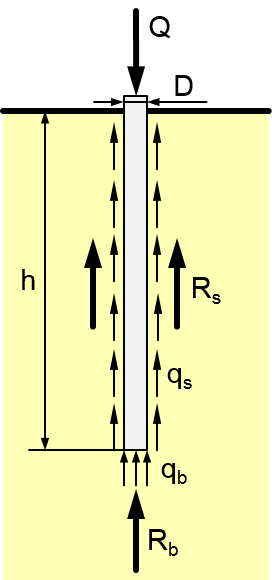
Sztywność pala w gruncie

Warto pamiętać, że opór pala zależy od wartości osiadania takiego pala. Zwykle przyjmuje się, że opór pala rośnie liniowo do granicznej wartości osiadania, po czym przyjmuje wartość stałą, czyli osiąga swoją nośność. Wartości osiadania granicznego mogą się różnić w zależności od przyjętej normy czy wytycznych. Tutaj nie będę tego szczegółowo rozwijał (więcej znajdziecie w Eurokodzie 7 lub w starej polskiej normie dot. fundamentów palowych PN-83/B-02482; źródła podałem na końcu tekstu). Zaadaptowałem też tutaj założenia niemieckich wytycznych „EA-Pfähle” dot. obliczania pali. Na poniższym rysunku pokazałem przykładową krzywą osiadania pala pod obciążeniem osiowym i jej składowe.

Sztywność pala w gruncie

Na podstawie tego rysunku możemy przyjąć trzy założenia:

  1. Nośność pala jest ograniczona i równa obciążeniu pala przy osiadaniu granicznym (s_{lim}),
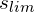  2. Składowa nośności podstawy pala rośnie liniowo do wartości osiadania granicznego,
  3. Składowa nośności pobocznicy pala rośnie liniowo do pewnej wartości osiadania (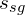s_{sg}) i następnie przyjmuje wartość stałą.

Uproszczony sposób określenia nośności pala

Jak określić nośność pala? Nie tak trudno. Normy i wytyczne podają dokładnie jak oszacować nośność pojedynczego pala lub grupy pali. Zasada jest taka, że sumujemy składowe nośności pala dla podstawy pala (R_b) i jego pobocznicy wg poniższego wzoru:

    \[R_k(s) = R_{b,k}(s) + R_{s,k}(s) = \eta_b q_{b,k} A_b + \sum_{}{}{\eta_s q_{s,k,i} A_{s,i}}\]

gdzie: R_{c,k} – charakterystyczna nośność pojedynczego pala, R_{b,k} – nośność podstawy pala, R_{s,k} – nośność pobocznicy pala, s – osiadanie pala, q_{b,k} – jednostkowa wytrzymałość gruntu pod podstawą, q_{s,k,i} – jednostkowa wytrzymałość gruntu wzdłuż pobocznicy w obrębie warstwie i, A_{s,i} – pole powierzchni pobocznicy pala (dla pala o przekroju okrągłym: A_{s,i} = πDh_i), \eta_b, \eta_s – współczynniki przyjmowane z tablic w zależności od typu pala lub parametrów gruntu (zależnie od przyjętej metody).

Widać wyraźnie, że składowa nośności pobocznicy pala zależna jest od liczby i parametrów warstw gruntu, w którym pal jest zagłębiony. Jest o tyle istotne, że w pewnych przypadkach nośność pala nie jest zwykłą sumą składowych. Ale o tym i o kilku innych rodzynkach napiszę pod koniec.

Dodatkowo, z racji, że dopuszczalna wartość osiadania pala s jest ograniczona (stany graniczne), zdolność pala do przenoszenia obciążeń nie rośnie w nieskończoność. Obciążenie jakie może przenieść pal przy granicznym (maksymalnym) osiadaniu jest jego nośnością. Jedno z metod określenia osiadania granicznego jest podejście pokazane poniżej:

  • Osiadanie graniczne głowicy pala wciskanego ze względu na wyczerpanie nośności[1]:

        \[s_{lim} = 0.10 D\]

  • Osiadanie głowicy pala, po którym wartość oporu pobocznicy pala jest stała (= nośność pobocznicy pala)[2]:

        \[s_{sg} = 0.5 R_{s,k}(s) [MN] \le 1\ cm\]

[1] wzór zaczerpnięty z Eurokodu 7, patrz: pkt. 7.6.1.1 (3),

[2] wzór zaczerpnięty z EA-Pfähle, patrz: pkt. 5.4.4, wzór (5.4) dla mikropali oraz pkt. 5.4.5, wzór (5.6) dla pali wbijanych. Dla pali wierconych można przyjmować s_{sg} = 0.5\ R_{s,k}(s_{sg})\ [MN] + 0.5\ [cm] \le 3\ [cm] – pkt. 5.4.6, wzór (5.10).

Można oczywiście stosować inną sprawdzoną metodę na określenie osiadania granicznego. Tutaj, z racji swojej prostoty, podałem metodę za EC7 i EA-Pfähle.

Sztywność pala jako podpory zastępczej – współczynnik sprężystości

Dotarliśmy w końcu do sedna. Czyli jak określić współczynnik sprężystości pala zagłębionego w gruncie jako podpory zastępczej? Nic prostszego. Sztywność pala wciskanego zagłębionego w gruncie to stosunek obciążenia jakie on przenosi do osiadania takiego pala w gruncie pod tym obciążeniem, tj.:

    \[k_s = \frac{R_{c,k}(s)}{s} = \frac{R_{c,k}(s_{sg})}{s_{sg}}\ [kN/m]\]

Jak widzicie, określenie zastępczej sztywności pala nie jest trudne. Należy przed tym znać jego nośność i graniczne osiadanie.

Zapis na newsletter

Przykład obliczeniowy

Zróbmy jeden przykład, przecież praktyka uczy :) Mamy pal wkręcany typu Atlas zagłębiony w gruncie na głębokość 6.0\ m i poniższe dane:

  • Średnica pala: D = 0.56\ m
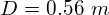
  • Grunt (podano kolejno: nr warstwy, miąższość , jednostkowa wytrzymałość gruntu wzdłuż pobocznicy pala oraz jednostkowa wytrzymałość gruntu pod podstawą pala):
Nr warstwy Miąższość q_{s,k,i} q_{b,k,i}
[-] [m] [kN/m2] [kN/m2]
(1) < 2.5 50.0 —
(2) 2.5 – 4.5 150.0 —
(3) > 4.5 100.0 2000.0
  • \eta_b = \eta_s = 1.00 (przyjęto wartość niekorzystną)

Mając wszystkie potrzebne dane możemy teraz określić sztywność pala wciskanego jako podpory zastępczej.

  • Pole podstawy pala:

    \[A_b = \cfrac{\pi D^2}{4} = \cfrac{3.14 \cdot 0.56^2}{4} = 0.246\ m2\]

  • Obwód pobocznicy:

    \[U_s = \pi D = 3.14 \cdot 0.56 = 1.758\ m\]

  • Nośność pobocznicy:
Nr warstwy q_{s,k,i} h_i A_{s,i} R_{s,k,i}[3]
[-] [kN/m2] [m] [m2] [kN]
(1) 50.0 2.50 4.40 219.9
(2) 150.0 2.00 3.52 527.5
(3) 100.0 1.50 2.64 263.8
Suma — 6.00 — 1011.1

[3] R_{s,k,i} = \sum_{}{}{\eta_s q_{s,k,i} A_{s,i}}

  • Nośność podstawy pala:

    \[R_{b,k} = A_b\ q_{b,k} = 0.246 \cdot 2000.0 = 492.4\ kN\]

  • Osiadanie pala:

    \[s_{sg} = 0.5 R_{s,k} [MN] + 0.5\ [cm] \le 3.0\ cm =\]

    \[= min(0.5\ \cdot\ 1.011 [MN] + 0.5\ [cm]; 3.0\ cm) = 1.01\ cm\]

    \[s_{lim} = 0.1 D = 0.1 \cdot 0.56 = 5.60\ cm\]

  • Nośność całkowita pala:
Osiadanie s/D R_{b,k} R_{s,k} R_k
[cm] [-] [kN] [kN] [kN]
0.00 0.00 0.0 0.0 0.0
1.01 0.02 88.4[4] 1011.1 1099.5
5.60 0.10 492.4 1011.1 1503.4

[4] wartość interpolowana

Na podstawie tych wyników możemy zbudować krzywą osiadania – rysunek poniżej.

Sztywność pala w gruncie

W naszym przykładzie sztywność podpory zastępczej, która modeluje pal Atlas wynosi:

    \[k_s = \cfrac{R_k(s)}{s} = \cfrac{1099.5\ kN}{1.01\ cm} = 108\ 861\ kN\]

Uwagi

Poniżej, jak obiecałem, zamieszczam dla Was jeszcze krótkie uzupełnienie, na które warto zwrócić uwagę. Uproszczony sposób, który przedstawiłem wyżej, jest łatwy w stosowaniu. Dzięki niemu możemy szybko zorientować się jaką sztywność powinny mieć podpory zastępcze zamodelowane zamiast pali.

Nie należy jednak podchodzić do tej procedury bezrefleksyjnie. Poniżej zestawiłem 3 ogólne uwagi, o których należy pamiętać przy obliczeniach pali fundamentowych. Nie wynikają one z samej metody, którą przedstawiłem, a raczej z zasad, o których mówią cytowane normy do projektowania.

Uwaga #1

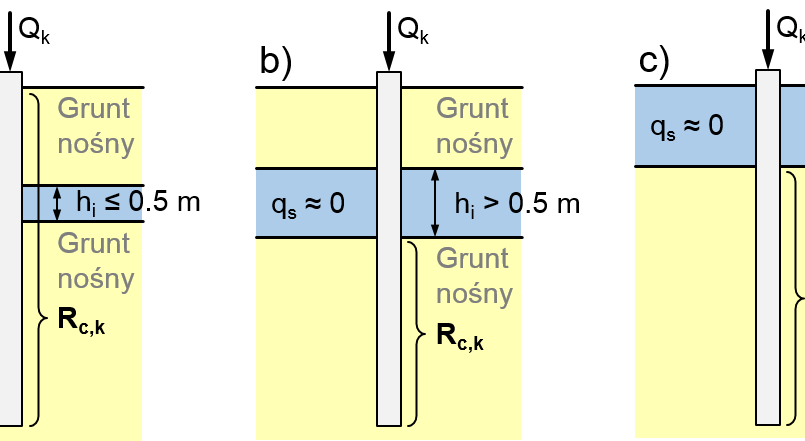
Może się tak zdarzyć, że wśród warstw gruntu występuje warstwa nienośna (np. grunt spoisty w stanie płynnym lub torf) i jej miąższość jest większa niż 0.5 m. Wtedy to składowa nośności pobocznicy pala musi zostać zredukowana – cała powierzchnia pobocznicy pala znajdująca się w warstwie nienośnej lub w warstwach powyżej nie jest wliczana do nośności pala.

Ma to związek z tzw. tarciem negatywnym i uwagą nr 2.

Uwaga #2

Tarcie negatywne (ujemne) na pobocznicy powstaje z powodu osiadania gruntu wokół pala. Grunt ten ciągnie pal ku dołowi, przez co obniża jego nośność. Może nawet dojść do sytuacji, gdzie tarcie negatywne całkowicie zredukuje tarcie (pozytywne) na pobocznicy pala. W takiej sytuacji nośność pala jest zredukowana do składowej nośności pod jego podstawą. Taka sytuacja może wystąpić w następujących przypadkach:

  • pal jest wprowadzany w warstwy nośne przez warstwy gruntów nieskonsolidowanych lub luźno usypanych, które osiadają pod wpływem własnego ciężaru,
  • pojawiło się dodatkowe obciążenie naziomu lub odwodnienie gruntu zalegającego wokół pala.

Uwaga #3

A co jeśli pal jest wyciągany? Jak wtedy określić jego sztywność w gruncie jako podporę zastępczą? Istnieje jedna zasadnicza różnica w stosunku do pala wciskanego. Otóż w przypadku pala wyciąganego składowa nośności podstawy pala jest równa 0, tzn. podstawa pala nie pracuje, ponieważ grunt nie przenosi naprężeń rozciągających. I oto cała filozofia :)

Jeżeli mamy do czynienia z palem wyciąganym i jedna z warstw gruntu jest nienośna (patrz uwaga 1), to należy uwzględnić opór pobocznicy również w warstwach leżących powyżej warstw nienośnych. Tarcie negatywne działa tutaj korzystnie.

Poniższy rysunek obrazuje opisane sytuacje.

Sztywność pala w gruncie

Źródła

  • PN-EN 1997-1:2008 Projektowanie geotechniczne. Część 1: Zasady ogólne + zmiany i załączniki krajowe,
  • PN-83/B-02482 Fundamenty budowlane. Nośność pali i fundamentów palowych,
  • Empfehlungen des Arbeitskreises „Pfähle” – EA-Pfähle (tłum.: Zalecenia komisji „Pale” – EA-Pale) Deutschen Gesellschaft für Geotechnik e.V., Ernst & Sohn, Berlin 2007.
Podziel się z innymi:

5 komentarzy

  • Hej Łukasz,

     

    w obliczeniach nie jest błąd? Ponieważ nośność pobocznicy pali jest wyznaczona jak dla osiadania 5,6cm a nie 1,01cm?

    Odpowiedz

  • Cześć, trafiłem na Twój blog szukając jak w prosty sposób określić sztywność poziomą pala w gruncie (słynne sprężynki). Istnieje wiele skomplikowanych metod. W Sofistiku znalazłem bardzo prostą metodę (pal jest zanurzony w półprzestrzeni dla której podaje się sztywność „k” zależną tylko od siecznego modułu odkształcenia gruntu „Es”; dla sztywności „k” można określić zmienność na głębokości pala zgodnie z 8.2.3 EA-Pfähle; program sam przyjmuje podparcia wzdłuż pala zależnie od średnicy pala). Czy masz jakieś doświadczenia w tym temacie?

    Odpowiedz

    • Tak, półprzestrzeń wydaje się najbardziej dokładna. Sam nie korzystałem z tego modułu Sofistika.
      To, co podałeś, to dotyczy pali w grupie. W uproszczonym przypadku sprowadzić to można do równania (6.5) w EA-Pfaehle, czyli ks,k = Es,k / D, gdzie D to średnica pala.
      Niestety sam nie mam tutaj dużo doświadczenia. Poszukaj u mostowców – oni na pewno w tym siedzą :)

      Odpowiedz

  • Hej, co do jednostek, ks= 1099,5 kN/ 1,01 cm = 109 343 kN/m a w zasadzie 108861,4 kN/m, pewnie zaokrąglenie w excelu.

    Odpowiedz

Dodaj komentarz

Twój adres e-mail nie zostanie opublikowany. Wymagane pola są oznaczone *